Exam 15: Functions of Several Variables
Exam 1: Functions and Applications159 Questions
Exam 2: Nonlinear Functions and Models92 Questions
Exam 3: The Mathematics of Finance137 Questions
Exam 4: Systems of Linear Equations and Matrices111 Questions
Exam 5: Matrix Algebra and Applications174 Questions
Exam 6: Linear Programming161 Questions
Exam 7: Sets and Counting154 Questions
Exam 8: Probability257 Questions
Exam 9: Random Variables and Statistics178 Questions
Exam 10: Introduction to the Derivative139 Questions
Exam 11: Techniques of Differentiation104 Questions
Exam 12: Applications of the Derivative88 Questions
Exam 13: The Integral66 Questions
Exam 14: Further Integration Techniques and Applications of the Integral118 Questions
Exam 15: Functions of Several Variables137 Questions
Exam 16: Trigonometric Models67 Questions
Select questions type
What point on the surface z is closest to the origin
Hint : Minimize the square of the distance from to the origin.
NOTE: Please enter your answer(s) in the form . If there is more than one answer, separate them with commas.
(Essay)
4.8/5  (36)
(36)
Let
What condition on H guarantees that f has a relative extremum at the point
(Short Answer)
4.9/5  (42)
(42)
Use Lagrange Multipliers to solve the problem.
Find the maximum value of subject to .
(Multiple Choice)
5.0/5  (42)
(42)
Write the integral with the order of integration reversed (changing the limits of integration as necessary).
(Multiple Choice)
4.9/5  (37)
(37)
Solve the given problem by using substitution.
Find the maximum value of subject to .
(Multiple Choice)
5.0/5  (35)
(35)
Use the given tabular representation of the function to compute . -5 197 185 -5 -9 191 100 -4 -20 201 225 -19 -19 216 235 -18
(Multiple Choice)
4.9/5  (31)
(31)
Use Lagrange Multipliers to solve the given problem.
Find the maximum value of subject to .
(Multiple Choice)
4.8/5  (31)
(31)
If positive electric charges of Q and q coulombs are situated at positions and , respectively, then the force of repulsion they experience is given by
Where , F is given in newtons, and all positions are measured in meters. Assume that a charge of 4 coulombs is situated at the origin and that a second charge of 14 coulombs is situated and moving in the y direction at 1.4 meters per second. How fast is the electrostatic force it experiences decreasing
NOTE: Please enter your answer without the units. Round the answer to the nearest trillion.
(Essay)
4.9/5  (37)
(37)
Your company manufactures two models of stereo speakers, the Ultra Mini and the Big Stack. Demand for each depends partly on the price of the other. If one is expensive then more people will buy the other. If p1 is the price per pair of the Ultra Mini and p2 is the price of the Big Stack, demand for the Ultra Mini is given by
Where q1 represents the number of pairs of Ultra Minis that will be sold in a year. The demand for the Big Stack is given by
Find the prices for the Ultra Mini and the Big Stack that will maximize your total revenue.
Round your answer to the nearest dollar.
(Multiple Choice)
4.7/5  (36)
(36)
Solve the given problem by using substitution.
Minimize subject to with , , .
(Multiple Choice)
4.8/5  (34)
(34)
Find , where and R is the indicated domain. (Remember that you often have a choice as to the order of integration.) 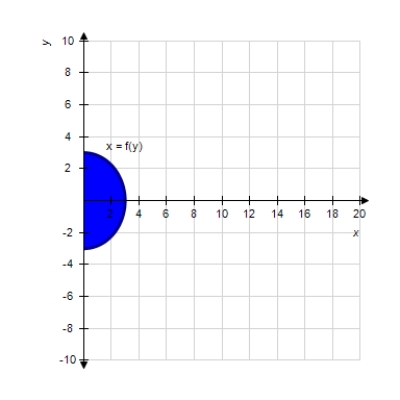
(Multiple Choice)
4.7/5  (31)
(31)
Showing 101 - 120 of 137
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)