Exam 15: Functions of Several Variables

Your latest CD - ROM drive is expected to sell between $q = 200,000 - p ^ { 2 }$ and $q = 230,000 - p ^ { 2 }$ Units if priced at p. You plan to set the price between $200 and $400. What are the maximum and minimum possible revenues you can make What is the average of all the possible revenues you can make

Calculate the values of $\frac { \partial f } { \partial x }$ , $\frac { \partial f } { \partial y }$ , and $\frac { \partial f } { \partial z }$ at $( 8,3,4 )$ . $f ( x , y , z ) = x y z$

Find the volume of the tetrahedron with corners at ( 0, 0, 0 ), ( 3, 0, 0 ), ( 0, 10, 0 ) and ( 0, 0, 8 ). ​

Choose the correct letter for each question. -neither

The burden of human made aerosol sulfate in the earth's atmosphere, in grams per square meter, is $B ( x , n ) = \frac { x n } { A }$ Where x is the total weight of aerosol sulfate emitted into the atmosphere per year and n is the number of years it remains in the atmosphere. A is the surface area of the earth, approximately $5 \times 10 ^ { 14 }$ square meters. Calculate the burden given the 1995 estimated values of $x = 2.8 \times 10 ^ { 14 }$ grams per year and $n = 20$ days. Enter the number of grams per square meter as a number without the units. Round to three decimal places.

The cost of controlling emissions at a firm goes up rapidly as the amount of emissions reduced goes up. Here is a possible model. $C ( x , y ) = 6,000 + 100 x ^ { 2 } + 25 y ^ { 2 }$ Where x is the reduction in sulfur emissions, y is the reduction in lead emissions (in pounds of pollutant per day), and C is the daily cost to the firm (in dollars) of this reduction. Government clean-air subsidies amount to $600 per pound of sulfur and $50 per pound of lead removed. How many pounds of pollutant should the firm remove each day to minimize the net cost (cost minus subsidy)

Sketch the graph of the function. $f ( x , y ) = 3 - x - y$

Sketch the graph of the function. $f ( x , y ) = 5 ( x + y )$

Solve the given problem by using substitution. Find the minimum value of $f ( x , y , z ) = 2 x ^ { 2 } + 2 x + y ^ { 2 } - y + z ^ { 2 } - z - 4$ subject to $z = 2 y$ .

Your weekly cost (in dollars) to manufacture x cars and y trucks is given by ​ $C ( x , y ) = 250,000 + 6,900 x + 3,300 y$ ​ Find $\frac { \partial C } { \partial x }$ , and $\frac { \partial C } { \partial y }$ . ​ NOTE: Please enter your answers without the units, separated by commas.

For the function $f ( x , y ) = x ^ { 2 } + 5 y ^ { 2 }$ Show the cross section at $x = 0$ .

Your on-line bookstore is in direct competition with Amazon.com, BN.com, and Borders.com. Your company's daily revenue in dollars is given by ​ $R ( x , y , z ) = 15,000 - 0.02 x - 0.01 y - 0.02 z + 0.0001 y z$ ​ where x, y, and z are the online daily revenues of Amazon.com, BN.com, and Borders.com, respectively. If Amazon.com and BN.com each show a daily revenue of $5,000, give an equation showing how your daily revenue depends on that of Borders.com.

Graph the function. $f ( x , y ) = 2.5 y ^ { 2 }$

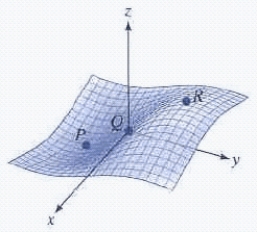
Classify each labeled point on the graph. ​ ​ Choose the correct letter for each question. ​ -a relative maximum

Calculate $\frac { \partial ^ { 2 } f } { \partial x ^ { 2 } }$ , $\frac { \partial ^ { 2 } f } { \partial y x }$ when defined. $f ( x , y ) = 4 x ^ { 0.9 } y ^ { 0.7 }$

For the function $f ( x , y ) = \frac { 3 x } { x ^ { 2 } - y ^ { 2 } }$ Find $f ( 0.6,0.5 )$ . Round to the nearest whole number if necessary.

In the table below, classify each highlighted value. 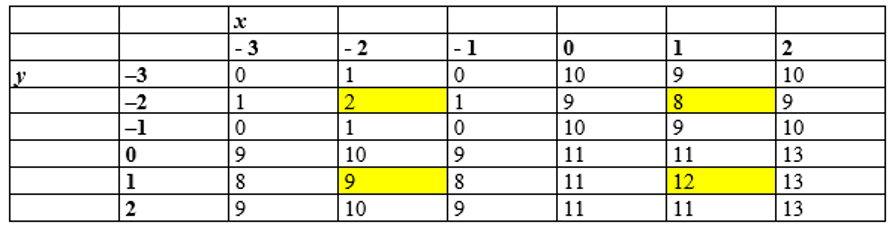-relative maximum

Choose the correct letter for each question. -interaction

In the table below, classify each highlighted value. ​ ​

Find the point on the given plane closest to $( 1,1,0 )$ . $2 x - 2 y - 4 z + 96 = 0$