Exam 12: Applications of the Derivative

A study of about 1800 U.S. colleges and universities resulted in the demand equation $q = 11,684 - 2.3 p$ Where q is the enrollment at a college or university and p is the average annual tuition (plus fees) it charges. The study also found that the average tuition charged by universities and colleges was $2,771. What is the corresponding elasticity of demand Round your answer to the two decimal places.

A general linear demand function has the form that follows. $q = n p + b$ (n and b constants, with $n \neq 0$ ) Obtain a formula for the price that maximizes revenue.

In 1965 the economist F.M. Scherer modeled the number, n, of patens produced by a firm as a function of the size, s, of the firm (measured in annual sales in millions of dollars). He came up with the following equation based on a study of 448 large firms. Round your answer to two decimal places. $n = - 3.93 + 132.61 s - 22.88 s ^ { 2 } + 1.311 s ^ { 3 }$ Find $\left. \frac { \mathrm { d } ^ { 2 } n } { \mathrm { ds } ^ { 2 } } \right| _ {= 4 }$ .

Your automobile assembly plant has a Cobb-Douglas production function given by $q = x ^ { 0.5 } y ^ { 0.5 }$ Where q is the number of automobiles it produced per year, x is the number of employees, and y is the daily operating budget (in dollars). Annual operating costs amount to an average of $30,000 per employee plus the operating budget of $\$ 300 y$ . Assume you wish to produce 1,500 automobiles per year at a minimum cost. How many employees should you hire

A cylindrical bucket is being filled with paint at a rate of $4 \frac { \mathrm { cm } ^ { 3 } } { \min }$ . How fast is the level rising when the bucket starts to overflow The bucket has a height of 40 cm and a radius of 10 cm. Round your answer to the three decimal places.

The area of a circular sun spot is growing at a rate of $600 \frac { \mathrm { km } ^ { 2 } } { \mathrm {~s} }$ . How fast is the radius growing at the instant when it equals 5,000 km Round your answer to three decimal places.

Find the exact location of all the relative and absolute extrema of the function. $f ( x ) = \sqrt { x } ( x - 21 ) , x \geq 0$ Select all correct answers.

Fair Weather Airlines will accept only bags for which the sum of the length and width is 51 inches, while the sum of length, height, and twice the width is 102 inches. What is the largest volume of the bag that it will accept Round your answer to the nearest whole number.

Find the exact location of all the relative and absolute maxima of the function. $f ( x ) = \frac { 8 } { x } - \frac { 4 } { x ^ { 2 } }$ Select all correct answers.

A general exponential demand function has the form to follow. $q = A e ^ { - m q }$ (A, m - nonzero constants) Obtain a formula for the elasticity of demand at a unit price of p.

My aunt and I were approaching the same intersection, she from the south and I from the west. She was travelling at a steady speed of 20 mph, while I was approaching the intersection at 80 mph. At a certain instant in time, I was $\frac { 1 } { 10 }$ of a mile from the intersection, while she was $\frac { 1 } { 20 }$ of a mile from it. How fast were we approaching each other at that instant Round your answer to the nearest whole number.

A packaging company is going to make closed boxes, with square bases, that hold 2,197 cubic centimeters. What are the dimensions of the box that can be built with the least material

Minimize $S = x + y$ with $x y = 25$ and both $\chi$ and $y > 0$ .

The graph of a function $f ( x ) = x ^ { 2 } \lef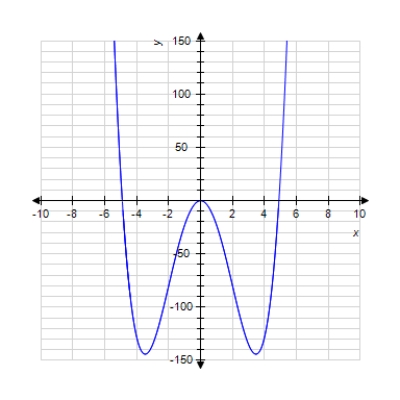t( x ^ { 2 } - 24 \right)$ is given. Find the coordinates of all points of inflection of this function (if any).

A rather flimsy spherical balloon is designed to pop at the instant its radius has reached 5 cm. Assuming the balloon is filled with helium at a rate of $10 \frac { \mathrm { cm } ^ { 3 } } { \mathrm {~s} }$ , calculate how fast the diameter is growing at the instant it pops. Round your answer to the three decimal places. The volume of a sphere of radius r is $V = \frac { 4 } { 3 } \pi r ^ { 3 }$ .

The consumer demand curve for tissues is given by $q = ( 92 - p ) ^ { 2 }$ Where p is the price per case of tissues and q is the demand in weekly sales. Determine the elasticity of demand E when the price is set at $30. Round the answer to the nearest hundredth.

For a rectangle with area 25 to have the smallest perimeter, what dimensions should it have ?

The volume of paint in a right cylindrical can is given by $V = 2 t ^ { 2 } - t$ , where t is time in seconds and V is the volume in cm³. How fast is the level rising when the height is 3 cm The can has a height of 5 cm and a radius of 3 cm. [Hint: To get h as a function of t, first solve the volume $V = \pi r ^ { 2 } h$ for h.] Round your answer to the nearest whole number. ?

A point on the graph of $y = \frac { 5 } { x }$ Is moving along the curve in such a way that its x-coordinate is increasing at a rate of 2 units per second. At what rate is the y-coordinate decreasing at the instant the y-coordinate is equal to 5

You have been hired as a marketing consultant to Big Book Publishing, Inc., and you have been approached to determine the best price for the hit calculus text by Whiner and Istanbul entitled Fun with Derivatives. You decide to make life easy and assume that the demand equation for Fun with Derivatives has the linear form $q = m p + b$ Where p is the price per book, q is the demand in annual sales, and m and b constants are certain constants you'll have to figure out. Your market studies reveal the following sales figures: when the price is set at $57 per book, the sales amount to 12,280 per year, when the price is set at $86 per book, the sales drop to 4,740 per year. Use these data to calculate the demand equation.