Exam 12: Applications of the Derivative
Exam 1: Functions and Applications159 Questions
Exam 2: Nonlinear Functions and Models92 Questions
Exam 3: The Mathematics of Finance137 Questions
Exam 4: Systems of Linear Equations and Matrices111 Questions
Exam 5: Matrix Algebra and Applications174 Questions
Exam 6: Linear Programming161 Questions
Exam 7: Sets and Counting154 Questions
Exam 8: Probability257 Questions
Exam 9: Random Variables and Statistics178 Questions
Exam 10: Introduction to the Derivative139 Questions
Exam 11: Techniques of Differentiation104 Questions
Exam 12: Applications of the Derivative88 Questions
Exam 13: The Integral66 Questions
Exam 14: Further Integration Techniques and Applications of the Integral118 Questions
Exam 15: Functions of Several Variables137 Questions
Exam 16: Trigonometric Models67 Questions
Select questions type
The estimated monthly sales of Mona Lisa paint-by-number sets is given by the formula
Where q is the demand in monthly sales and p is the retail price in yen. Determine the elasticity of demand E when the retail price is set at 2 yen.
(Multiple Choice)
4.8/5  (39)
(39)
A baseball diamond is a square with side 90 ft. A batter at the home base hits the ball and runs toward first base with a speed of . At what rate is his distance from third base increasing when he is halfway to first base ? Round your answer to the one decimal place. 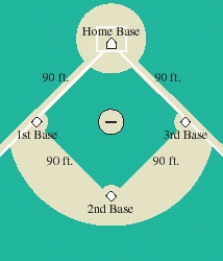
(Multiple Choice)
4.7/5  (34)
(34)
You have been hired as a marketing consultant to Big Book Publishing, Inc., and you have been approached to determine the best price for the hit calculus text by Whiner and Istanbul entitled Fun with Derivatives. You decide to make life easy and assume that the demand equation for Fun with Derivatives has the linear form
Where p is the price per book, q is the demand in annual sales, and m and b constants are certain constants you'll have to figure out. Your market studies reveal the following sales figures: when the price is set at $42 per book, the sales amount to 50,560 per year, when the price is set at $93 per book, the sales drop to 34,240 per year. Now estimate the unit price in order to maximize annual revenue and predict what Big Book Publishing's annual revenue will be at that price. Round your answers to the nearest dollar.
(Multiple Choice)
4.8/5  (35)
(35)
The HMS Dreadnaught is 20 miles north of Montauk and steaming due north at 10 mph, while the USS Mona Lisa is 25 miles east of Montauk and steaming due east at an even 15 mph. How fast is their distance apart increasing Round your answer to the nearest whole number.
(Multiple Choice)
4.9/5  (35)
(35)
For a rectangle with perimeter 32 to have the largest area, what dimensions should it have ?
(Multiple Choice)
4.9/5  (33)
(33)
A company finds that the number of new products it develops per year depends on the size if its annual R&D budget, x (in thousands of dollars), according to the following formula. Round your answer to one decimal places.
Find .
(Multiple Choice)
4.9/5  (34)
(34)
The consumer demand curve for Professor Stefan Schwartzenegger dumbbells is given by
Where p is the price per dumbbell and q is the demand in weekly sales. Find the price Professor Schwartzenegger should charge for his dumbbells in order to maximize revenue.
(Multiple Choice)
4.7/5  (35)
(35)
A fried chicken franchise finds that the demand equation for its new roast chicken product, "Roasted Rooster", is given by
Where p is the price (in dollars) per quarter-chicken serving and q is the number of quarter-chicken servings that can be sold per hour at this price. Express q as a function of p, and find the elasticity of demand when the price is set at $5 per serving.
(Multiple Choice)
4.7/5  (34)
(34)
A right conical circular vessel is being filled with green industrial waste at a rate of 200 cubic meters per second. How fast is the level rising after cubic meters have been poured in (The cone has height 75 m and radius 45 m at its brim. The volume of a cone of height h and cross-sectional radius r at its brim is given by .) Round your answer to the one decimal place.
(Multiple Choice)
4.9/5  (47)
(47)
The cost of controlling emissions at a firm goes up rapidly as the amount of emissions reduced goes up. Here is a possible model:
Where q is the reduction in emissions (in pounds of pollutant per day) and C is the daily cost to the firm (in dollars) of this reduction. Government clean air subsidies amount to $750 per pound of pollutant removed. How many pounds of pollutant should the firm remove each day to minimize net cost (cost minus subsidy)
(Multiple Choice)
4.8/5  (29)
(29)
Find the exact location of all absolute extrema of the function. Round your answers to four decimal places.
Select all correct answers.
(Multiple Choice)
4.9/5  (32)
(32)
The automobile assembly plant you manage has a Cobb-Douglas production function given by
Where P is the number of automobiles the plant produces per year, x is the number of employees, and y is the daily operating budget (in dollars). You maintain a production level of 3,500 automobiles per year. If you currently employ 100 workers and are hiring new workers at a rate of 10 per year, how fast is your daily operating budget changing Round your answer to the nearest cent.
(Multiple Choice)
5.0/5  (40)
(40)
A study found that the divorce rate d (given as a percentage) appears to depend on the ratio r of available men to available women. This function can be approximated by
There are currently 0.8 available men per available woman in Littleville, and this ratio is increasing by 0.1 per year. At what percent is the divorce rate decreasing
(Multiple Choice)
4.9/5  (40)
(40)
Find the exact location of all the relative and absolute extrema of the function with domain .
(Multiple Choice)
5.0/5  (37)
(37)
Showing 41 - 60 of 88
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)