Exam 11: Multifactor Analysis of Variance
Exam 1: Overview and Descriptive Statistics15 Questions
Exam 2: Probability16 Questions
Exam 3: Discrete Random Variables and Probability Distributions22 Questions
Exam 4: Continuous Random Variables and Probability Distributions17 Questions
Exam 5: Joint Probability Distributions and Random Samples19 Questions
Exam 6: Point Estimation28 Questions
Exam 7: Statistical Intervals Based on a Single Sample59 Questions
Exam 8: Tests of Hypotheses Based on a Single Sample92 Questions
Exam 9: Inferences Based on Two Samples73 Questions
Exam 10: The Analysis of Variance43 Questions
Exam 11: Multifactor Analysis of Variance62 Questions
Exam 12: Simple Linear Regression and Correlation106 Questions
Exam 13: Nonlinear and Multiple Regression77 Questions
Exam 14: Goodness-Of-Fit Tests and Categorical Data Analysis40 Questions
Exam 15: Distribution-Free Procedures66 Questions
Exam 16: Quality Control Methods86 Questions
Select questions type
In the fixed effects model with interaction, assume that there are 3 levels of factor A, 2 levels of factor B, and 3 observations for each of the six combinations of levels of the two factors. Then the critical value for testing the null hypothesis of no interaction between the levels of the two factors at the .05 significance level is
(Multiple Choice)
4.8/5  (34)
(34)
In a two-factor experiment where factor A consists of I levels, factor B consists of J levels, and there is only one observation on each of the IJ treatments, SSE has __________ degrees of freedom.
(Short Answer)
4.9/5  (36)
(36)
Assume the existence of I parameters and J parameters such that The model specified by the above equations is called an __________ model because each mean response is the __________ of an effect due to factor A at level and an effect due to factor B at level .
(Short Answer)
4.8/5  (31)
(31)
In the three-factor fixed effects model, assume that there are 4 levels of factor A, 2 levels of factor B, 4 levels of factor C, and 3 observations for each combination of levels of the three factors. Then, the number of degrees of freedom for the three-factor interaction sum of squares (SSABC) is
(Multiple Choice)
4.8/5  (40)
(40)
In the fixed effects model with interaction, assume that there are I levels of factor A, J levels of factor B, and K observations (replications) for each of the IJ combinations of levels of the two factors. Then SST (the total sum of squares) has df = __________.
(Short Answer)
4.9/5  (32)
(32)
The accompanying data was obtained in an experiment to investigate whether compressive strength of concrete cylinders depends of the type of capping material used or variability in different batches. Each number is a cell total
(Essay)
4.9/5  (33)
(33)
The following equation SST = SSA + SSB +SSC + SSAB + SSAC + SSBC + SSABC + SSE applies to which ANOVA model?
(Multiple Choice)
4.8/5  (31)
(31)
A data from an experiment to assess the effects of vibration (A), temperature cycling (B), altitude cycling (C), and temperature for altitude cycling and firing (D) on thrust duration are shown below. Use the Yates method to obtain sums of squares and the ANOVA table. Then assume that three- and four-factor interactions are absent, pool the corresponding sums of squares to obtain an estimate of and test all appropriated hypotheses at level .05. 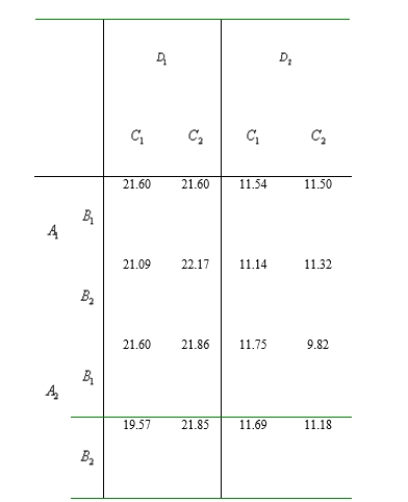
(Essay)
4.8/5  (37)
(37)
Which of the following statements are not true regarding the model where
(Multiple Choice)
4.8/5  (39)
(39)
In an experiment to assess the effects of curing time (factor A) and type of mix (factor B) on the compressive strength of hardened cement cubes, three different curing times were used in combination with four different mixes, with three observations obtained for each of the 12 curing time-mix combinations. The resulting sums of squares were computed to be SSA = 30,763.0, SSB = 34,185.6, SSE = 97,436.8, and SST = 205,966.6.
a. Construct an ANOVA table.
b. Test at level .05 the null hypothesis
(no interaction of factors) against
c. Test at level .05 the null hypothesis
(factor A main effects are absent) against
d. Test
at least one
using a level .05 test.
e. The values of the
Use Tukey's procedure to investigate significant differences among the three curing times.
(Essay)
4.8/5  (37)
(37)
A two-factor experiment where factor A consists of I levels, factor B consists of J levels, and there is only one observation on each of the IJ treatments, can be represented by the model . Which of the following is the correct form in testing the null hypothesis that the different levels of factor A have no effect on true average response?
(Multiple Choice)
4.7/5  (30)
(30)
In two-factor ANOVA, additivity means that the difference in true average responses for any two levels of one of the factors is the same for each level of the other factor. When additivity does not hold, we say that there is __________ between the different levels of the factors.
(Short Answer)
4.9/5  (45)
(45)
In the three-factor fixed effects model, assume that there are 3 levels for each of the three factors A, B, and C, and 2 observations for each combination of levels of the three factors. Then the number of degrees of freedom for the error sum of squares (SSE) is
(Multiple Choice)
4.7/5  (33)
(33)
The current (in ) necessary to produce a certain level of brightness of a television tube was measured for two different types of glass and three different types of phosphor, resulting in the accompanying data: Phosphor Type Glass 1 280,290,285 300,310,295 270,285,290 Type 2 230,235,240 260,240,235 220,225,230 Assuming that both factors are fixed, test at level .01. Then if cannot be rejected, test the two sets of main effect hypotheses.
(Essay)
4.8/5  (35)
(35)
An experiment in which there are p factors, each at two levels, is referred to as a
(Essay)
4.9/5  (35)
(35)
Showing 41 - 60 of 62
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)