In a diet test, each of four diet programs is applies to a sample of people. At the end of three weeks, the amount of pounds people lost is shown below. $\text { Diet Program } $ $\begin{array} { | c | c | c | c | } \hline 1 & 2 & 3 & 4 \\ \hline 12 & 19 & 16 & 28 \\ \hline 6 & 10 & 20 & 17 \\ \hline 18 & 13 & 26 & 22 \\ \hline 23 & 20 & 19 & 16 \\ \hline & 25 & & 20 \\ \hline \end{array}$ Test to determine whether there is enough evidence at the 5% significance level to infer that at least two population locations differ.

@#LAT-DLM& The locations of all four pop

In a Kruskal-Wallis test, the following statistics were obtained: T1 = 55, n1 = 5, T2 = 54, n2 = 5, T3 = 54, n3 = 5, T4 = 47, n4 = 5. Conduct the test at the 5% significance level.

@#LAT-DLM& The locations of all four populations a

Exam 21: Nonparametric Techniques

A fitness centre employs 4 different fitness instructors. Management would like to investigate if the different fitness instructors are getting different results with their team members. The number of kilograms lost per member over the last twelve months is recorded and divided by fitness instructor they were using. A table of fitness instructors with kilograms lost by each individual member, is given below. Can you advise management if the fitness instructors are consistent, (ie: test that at least two populations differ), at the 5% level of significance. Fitness instructor 13 15 18 9 9 10 15 10 16 15 17 6 12 14 18 6 15 13 8

Free

(Essay)

4.8/5

(37)

Question 1

Correct Answer:

Verified

$\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\text { Fitness instrictor }$
$\begin{array}{|c|c|c|c|c|c|c|r|}\hline \text { A } & \text { Rank } & \text { B } & \text { Rank } & \text { C } & \text { Rark } & \text { D } & \text { Rank } \\\hline 13 & 9.5 & 15 & 13.5 & 18 & 18.5 & 9 & 4.5 \\\hline 9 & 4.5 & 10 & 6.5 & 15 & 13.5 & 10 & 6.5 \\\hline 16 & 16 & 15 & 13.5 & 17 & 17 & 6 & 1.5 \\\hline 12 & 8 & 14 & 11 & 18 & 18.5 & 6 & 1.5 \\\hline 15 & 13.5 & & & 13 & 9.5 & & \\\hline 8 & 3 & & & & & & \\\hline 6 & 54.5 & 4 & 44.5 & 5 & 77 & 4 & 14 \\\hline & 495.04 & & 495.06 & & 1185.8 & & 49 \\\hline \text { Sum } & 2175.9 & & & & & & \\\hline\end{array}$
$H _ { 0 } :$ The locations of all four populations are the same. $H _ { 1 } :$ At least two populations differ.
Rejection region: H > $\quad \quad \quad \quad \quad \quad \quad \quad \text { Fitness instrictor } \begin{array}{|c|c|c|c|c|c|c|r|} \hline \text { A } & \text { Rank } & \text { B } & \text { Rank } & \text { C } & \text { Rark } & \text { D } & \text { Rank } \\ \hline 13 & 9.5 & 15 & 13.5 & 18 & 18.5 & 9 & 4.5 \\ \hline 9 & 4.5 & 10 & 6.5 & 15 & 13.5 & 10 & 6.5 \\ \hline 16 & 16 & 15 & 13.5 & 17 & 17 & 6 & 1.5 \\ \hline 12 & 8 & 14 & 11 & 18 & 18.5 & 6 & 1.5 \\ \hline 15 & 13.5 & & & 13 & 9.5 & & \\ \hline 8 & 3 & & & & & & \\ \hline 6 & 54.5 & 4 & 44.5 & 5 & 77 & 4 & 14 \\ \hline & 495.04 & & 495.06 & & 1185.8 & & 49 \\ \hline \text { Sum } & 2175.9 & & & & & & \\ \hline \end{array} H _ { 0 } : The locations of all four populations are the same. H _ { 1 } : At least two populations differ. Rejection region: H > 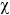2 0.05, 3 = 7.81 Calculated H = 8.71 Conclusion: Reject Ho and accept HA at 5% significance level. Conclude that there is significant evidence that the different trainers are providing different weight loss results.$ ² _0.05_,₃ = 7.81
Calculated H = 8.71
Conclusion: Reject Ho and accept H_A at 5% significance level. Conclude that there is significant evidence that the different trainers are providing different weight loss results.

Ten business people who fly frequently from Melbourne to Sydney were asked to rank four airlines in terms of the quality of service. The people assigned scores using a 5-point Likert scale where: 1 = bad, 2 = poor, 3 = average, 4 = good, and 5 = excellent. The results are shown below. $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\text { Airline }$ Person A B C D 1 5 5 2 1 2 3 3 4 2 3 2 3 4 3 4 1 1 4 3 5 4 1 5 3 6 2 3 4 2 7 1 3 5 2 8 3 3 5 1 9 1 3 5 2 10 2 4 3 1 Using the appropriate statistical table, what statement can be made about the p-value for the test?

Free

(Short Answer)

4.8/5

(28)

Question 2

Correct Answer:

Verified

p-value < 0.005.

The following data were generated from a randomised blocked experiment. Conduct a Friedman test at the 5% significance level to determine if at least two population locations differ. Treatment Block A Rank B C Rank D 1 70 80 50 65 2 50 87 52 81 3 69 97 75 83 4 65 72 62 73 5 58 87 52 62

Free

(Essay)

4.8/5

(34)

Question 3

Correct Answer:

Verified

$\begin{array} { | c | c | c | c | c | c | c | c | c | } \hline & { \text { Treatment } } & \\\hline \text { Block } & \text { A } & \text { Rank } & \text { B } & \text { Rank } & \text { C } & \text { Rank } & \text { D } & \text { Rank } \\\hline 1 & 70 & 3 & 80 & 4 & 50 & 1 & 65 & 2 \\\hline 2 & 50 & 1 & 87 & 4 & 52 & 2 & 81 & 3 \\\hline 3 & 69 & 1 & 97 & 4 & 75 & 2 & 83 & 3 \\\hline 4 & 65 & 2 & 72 & 3 & 62 & 1 & 73 & 4 \\\hline 5 & 58 & 2 & 87 & 4 & 52 & 1 & 62 & 3 \\\hline \text { Sum } & & 9 & & 19 & & 7 & & 15 \\\hline \text { Sum squared } & & 81 & & 361 & & 49 & & 225 \\\hline \text { Sum of squares } & & 716 & & & & & & \\\hline\end{array}$ $H _ { 0 } :$ The locations of all four populations are the same. $H _ { 1 } :$ At least two population locations differ.
Rejection region: $F _ { r } > \chi _ { 0.05,3 } ^ { 2 } = 7.8147$ .
Test statistic: F_r = 10.92
Conclusion: Reject the null hypothesis and accept the alternative hypothesis at the 5% significance level and conclude that at least two population locations differ significantly.

In a Kruskal-Wallis test, the following statistics were obtained: T₁ = 55, n₁ = 5, T₂ = 54, n₂ = 5, T₃ = 54, n₃ = 5, T₄ = 47, n₄ = 5. What is the most accurate statement that can be made about the p-value of this test?

(Essay)

4.9/5

(30)

Question 4

Apply the Friedman test to the following table of ordinal data to determine whether we can infer at the 5% significance level that at least two population locations differ. $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\text { Treatment }$ Block A B C D i 2 5 3 1 iii 1 4 5 4 iii 3 4 2 2 iv 2 5 4 1 1 5 3 5

(Essay)

4.8/5

(36)

Question 5

The Kruskal-Wallis test statistic can be approximated by a Chi-squared distribution with k - 1 degrees of freedom (where k is the number of populations) whenever the sample sizes are all greater than or equal to:

(Multiple Choice)

4.9/5

(43)

Question 6

A movie critic wanted to determine whether or not moviegoers of different age groups evaluated a movie differently. With this objective, he commissioned a survey that asked people their ratings of their most recently watched movies. The rating categories were: 1 = terrible. 2 = fair. 3 = good. 4 = excellent. Each respondent was also asked to categorise his or her age as either: 1 = teenager. 2 = young adult (20-34). 3 = middle age (35-50). 4 = senior (over 50). The results are shown below. $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\text { Movie Ratings }$ Teenager Young Adult Middle Age Senior 3 2 3 3 4 3 2 4 3 3 1 4 3 2 2 3 3 2 2 3 4 1 3 4 2 3 1 4 4 2 4 3 Which test the movie critic can use in this situation?

(Short Answer)

4.8/5

(30)

Question 7

Use the 5% significance level to test the hypotheses. $H _ { 0 } :$ The two population locations are the same $H _ { 1 } :$ The location of population A is to the left of the location of population B, given that the data below are drawn from a matched pairs experiment. Matched Pair 1 2 3 4 5 6 7 8 A 8 10 11 7 6 7 13 10 B 6 9 12 10 12 10 5 8

(Essay)

4.8/5

(28)

Question 8

Which of the following are statistical methods that require few assumptions, if any, about the distribution of the population?

(Multiple Choice)

4.9/5

(34)

Question 9

The marketing manager of a pizza chain is in the process of examining some of the demographic characteristics of her customers. In particular, she would like to investigate the belief that the ages of the customers of pizza parlours, hamburger emporiums and fast-food chicken restaurants are different. As an experiment, the ages of eight customers of each of the restaurants are recorded and listed below. From previous analysis we know that the ages are not normally distributed. $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\text { Customer Age }$ Pizza Hamburger Chicken 23 26 25 19 20 28 25 18 36 17 35 23 36 33 39 25 25 27 28 19 38 31 17 31 Do these data provide enough evidence at the 10% significance level to infer that there are differences in age among the customers of the three restaurants?

(Essay)

4.9/5

(34)

Question 10

In a normal approximation to the Wilcoxon signed rank sum test, the test statistic is calculated as z = 1.59. For a two-tail test, the p-value is:

(Multiple Choice)

4.7/5

(43)

Question 11

The non-parametric tests discussed in your textbook (Wilcoxon rank sum test, sign test, Wilcoxon signed rank sum test, Kruskal-Wallis test and Friedman test) all require that the probability distributions be:

(Multiple Choice)

4.8/5

(41)

Question 12

A statistics course co-ordinator has decided to incorporate team based learning in tutorials. Each tutorial class of 30 students are grouped into 5 teams of 6 members each. The teams have one group project which is assessed out of 30 marks. There are three tutorial classes in this statistics course, with 5 teams each. Each tutorial class is taught by a different tutor. Each tutor marks their team's projects. The course coordinator wants to ascertain if marking is consistent by the three different tutors. The course coordinator has tabled each teams mark by tutor so as to conduct a Kruskal-Wallis test to determine whether there is enough evidence at the 10% significance level to infer that at least two of the populations represented by the samples below differ. That is, use this test to determine if at least two of the tutor's marks for team's projects differ. Sample Tutor A Tutor B Tutor C 23 28 20 22 27 22 25 27 19 20 19 21 18 20 20

(Essay)

4.9/5

(31)

Question 13

The Kruskal-Wallis test is applied to compare two or more populations when the samples are independent and the data are ordinal or numerical and non-normal.

(True/False)

5.0/5

(38)

Question 14

The general manager of a frozen TV dinner maker must decide which one of four new dinners to introduce to the market. He decides to perform an experiment to help make a decision. Each dinner is sampled by ten people who then rate the product on a 7-point scale, where 1 = poor, and 7 = excellent. The results are shown below. $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\text { Taste Ratings }$ Respondent Dinner 1 Dinner 2 Dinner 3 Dinner 4 1 6 6 4 5 2 5 5 2 4 3 7 7 3 4 4 6 6 5 4 5 7 6 4 3 6 7 5 3 5 7 6 4 3 4 8 5 6 4 6 9 4 4 3 5 10 7 5 6 4 Which test can the general manager use to help him make a decision?

(Short Answer)

4.8/5

(30)

Question 15

A one-sample t-test is the parametric counterpart of the Friedman test for randomised block experimental design.

(True/False)

4.9/5

(33)

Question 16

In a diet test, each of four diet programs is applies to a sample of people. At the end of three weeks, the amount of pounds people lost is shown below. $\text { Diet Program }$ 1 2 3 4 12 19 16 28 6 10 20 17 18 13 26 22 23 20 19 16 25 20 Test to determine whether there is enough evidence at the 5% significance level to infer that at least two population locations differ.

(Essay)

4.8/5

(32)

Question 17

In a Kruskal-Wallis test, the following statistics were obtained: T₁ = 55, n₁ = 5, T₂ = 54, n₂ = 5, T₃ = 54, n₃ = 5, T₄ = 47, n₄ = 5. Conduct the test at the 5% significance level.

(Essay)

4.9/5

(28)

Question 18

The marketing manager of a pizza chain is in the process of examining some of the demographic characteristics of her customers. In particular, she would like to investigate the belief that the ages of the customers of pizza parlours, hamburger emporiums and fast-food chicken restaurants are different. As an experiment, the ages of eight customers of each of the restaurants are recorded and listed below. From previous analysis we know that the ages are not normally distributed. $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\text { Customer Age }$ Pizza Hamburger Chicken 23 26 25 19 20 28 25 18 36 17 35 23 36 33 39 25 25 27 28 19 38 31 17 31 Using the appropriate statistical table, what statement can be made about the p-value for the test?

(Essay)

4.9/5

(39)

Question 19

A non-parametric test is one that makes no assumptions about the specific shape of the population from which a sample is drawn.

(True/False)

4.9/5

(35)

Question 20

The following data were generated from a randomised blocked experiment. Conduct a Friedman test at the 5% significance level to determine if at least two population locations differ. Treatment Block A Rank B C Rank D 1 70 80 50 65 2 50 87 52 81 3 69 97 75 83 4 65 72 62 73 5 58 87 52 62

In a Kruskal-Wallis test, the following statistics were obtained: T₁ = 55, n₁ = 5, T₂ = 54, n₂ = 5, T₃ = 54, n₃ = 5, T₄ = 47, n₄ = 5. What is the most accurate statement that can be made about the p-value of this test?

The Kruskal-Wallis test statistic can be approximated by a Chi-squared distribution with k - 1 degrees of freedom (where k is the number of populations) whenever the sample sizes are all greater than or equal to:

Which of the following are statistical methods that require few assumptions, if any, about the distribution of the population?

In a normal approximation to the Wilcoxon signed rank sum test, the test statistic is calculated as z = 1.59. For a two-tail test, the p-value is:

The non-parametric tests discussed in your textbook (Wilcoxon rank sum test, sign test, Wilcoxon signed rank sum test, Kruskal-Wallis test and Friedman test) all require that the probability distributions be:

The Kruskal-Wallis test is applied to compare two or more populations when the samples are independent and the data are ordinal or numerical and non-normal.

A one-sample t-test is the parametric counterpart of the Friedman test for randomised block experimental design.

In a Kruskal-Wallis test, the following statistics were obtained: T₁ = 55, n₁ = 5, T₂ = 54, n₂ = 5, T₃ = 54, n₃ = 5, T₄ = 47, n₄ = 5. Conduct the test at the 5% significance level.

A non-parametric test is one that makes no assumptions about the specific shape of the population from which a sample is drawn.

What Is Statistics

Types of Data, Data Collection and Sampling

Graphical Descriptive Methods Nominal Data

Graphical Descriptive Techniques Numerical Data

Numerical Descriptive Measures

Probability

Random Variables and Discrete Probability Distributions

Continuous Probability Distributions

Statistical Inference: Introduction

Sampling Distributions

Estimation: Describing a Single Population

Estimation: Comparing Two Populations

Hypothesis Testing: Describing a Single Population

Hypothesis Testing: Comparing Two Populations

Inference About Population Variances

Analysis of Variance

Additional Tests for Nominal Data: Chi-Squared Tests

Simple Linear Regression and Correlation

Multiple Regression

Model Building

Statistical Inference: Conclusion

Time-Series Analysis and Forecasting

Index Numbers

Decision Analysis

Filters

Exam 21: Nonparametric Techniques

The following data were generated from a randomised blocked experiment. Conduct a Friedman test at the 5% significance level to determine if at least two population locations differ. Treatment Block A Rank B C Rank D 1 70 80 50 65 2 50 87 52 81 3 69 97 75 83 4 65 72 62 73 5 58 87 52 62

In a Kruskal-Wallis test, the following statistics were obtained: T1 = 55, n1 = 5, T2 = 54, n2 = 5, T3 = 54, n3 = 5, T4 = 47, n4 = 5. What is the most accurate statement that can be made about the p-value of this test?

The Kruskal-Wallis test statistic can be approximated by a Chi-squared distribution with k - 1 degrees of freedom (where k is the number of populations) whenever the sample sizes are all greater than or equal to:

Which of the following are statistical methods that require few assumptions, if any, about the distribution of the population?

In a normal approximation to the Wilcoxon signed rank sum test, the test statistic is calculated as z = 1.59. For a two-tail test, the p-value is:

The non-parametric tests discussed in your textbook (Wilcoxon rank sum test, sign test, Wilcoxon signed rank sum test, Kruskal-Wallis test and Friedman test) all require that the probability distributions be:

The Kruskal-Wallis test is applied to compare two or more populations when the samples are independent and the data are ordinal or numerical and non-normal.

A one-sample t-test is the parametric counterpart of the Friedman test for randomised block experimental design.

In a Kruskal-Wallis test, the following statistics were obtained: T1 = 55, n1 = 5, T2 = 54, n2 = 5, T3 = 54, n3 = 5, T4 = 47, n4 = 5. Conduct the test at the 5% significance level.

A non-parametric test is one that makes no assumptions about the specific shape of the population from which a sample is drawn.

What Is Statistics

Types of Data, Data Collection and Sampling

Graphical Descriptive Methods Nominal Data

Graphical Descriptive Techniques Numerical Data

Numerical Descriptive Measures

Probability

Random Variables and Discrete Probability Distributions

Continuous Probability Distributions

Statistical Inference: Introduction

Sampling Distributions

Estimation: Describing a Single Population

Estimation: Comparing Two Populations

Hypothesis Testing: Describing a Single Population

Hypothesis Testing: Comparing Two Populations

Inference About Population Variances

Analysis of Variance

Additional Tests for Nominal Data: Chi-Squared Tests

Simple Linear Regression and Correlation

Multiple Regression

Model Building

Statistical Inference: Conclusion

Time-Series Analysis and Forecasting

Index Numbers

Decision Analysis

Filters

In a Kruskal-Wallis test, the following statistics were obtained: T₁ = 55, n₁ = 5, T₂ = 54, n₂ = 5, T₃ = 54, n₃ = 5, T₄ = 47, n₄ = 5. What is the most accurate statement that can be made about the p-value of this test?

In a Kruskal-Wallis test, the following statistics were obtained: T₁ = 55, n₁ = 5, T₂ = 54, n₂ = 5, T₃ = 54, n₃ = 5, T₄ = 47, n₄ = 5. Conduct the test at the 5% significance level.