Exam 13: Nonlinear Optimization Models
Exam 1: Introduction49 Questions
Exam 2: Descriptive Statistics84 Questions
Exam 3: Data Visualization69 Questions
Exam 4: Descriptive Data Mining56 Questions
Exam 5: Probability: an Introduction to Modeling Uncertainty62 Questions
Exam 6: Statistical Inference62 Questions
Exam 7: Linear Regression71 Questions
Exam 8: Time Series Analysis and Forecasting58 Questions
Exam 9: Predictive Data Mining40 Questions
Exam 10: Spreadsheet Models64 Questions
Exam 11: Linear Optimization Models58 Questions
Exam 12: Integer Linear Optimization Models56 Questions
Exam 13: Nonlinear Optimization Models55 Questions
Exam 14: Monte Carlo Simulation59 Questions
Exam 15: Decision Analysis58 Questions
Select questions type
A(n) __________ is a set of points defining the minimum possible risk for a set of return values.
(Multiple Choice)
4.9/5  (34)
(34)
A feasible solution is __________ if there are no other feasible points with a better objective function value in the entire feasible region.
(Multiple Choice)
4.8/5  (35)
(35)
A ____________ is the shadow price of a binding simple lower or upper bound on the decision variable.
(Multiple Choice)
4.9/5  (35)
(35)
The reduced gradient is analogous to the ___________ for linear models.
(Multiple Choice)
4.9/5  (36)
(36)
A nonlinear function with term to the power of two is known as a
(Multiple Choice)
4.8/5  (30)
(30)
Excel Solver's __________ is based on a method that searches for an optimal solution by iteratively adjusting a population of candidate solutions.
(Multiple Choice)
4.8/5  (32)
(32)
Using the graph below, which of the following is true of the above function? 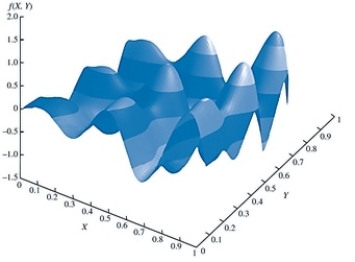
(Multiple Choice)
4.8/5  (36)
(36)
If the portfolio variance were equal to zero, the amount of risk would be
(Multiple Choice)
4.8/5  (29)
(29)
Jim must solve a nonlinear optimization problem where point A should be within a radius of 15 centimeters from each of the points B, C, D, E and F. The decision variables are defined as below.
X = horizontal coordinate of point A
Y = vertical coordinate of point A
The data on the distances is given below: Horizontal Coordinate Vertical Coordinate B 9 11 C 14 18 D 18 22 E 13 16 F 17 21 Formulate and solve a model that minimizes the maximum distance from point A to each of the points B, C, D, E, and F. Round all your answers to three decimal places.
(Essay)
4.8/5  (44)
(44)
Consider the following data on the returns from bonds. nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; nbsp; Year Bon d 1 0.20 0.126 0.321 -0.39 -0.67 0.135 0.52 0.75 Bon d 2 0.128 0.21 0.325 -0.243 0.169 0.125 0.304 0.286 Bon d 3 0.167 0.27 0.426 -0.84 0.143 -0.46 0.147 0.704
a. Construct the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur.
b. Solve the model using Excel Solver.
(Essay)
4.9/5  (32)
(32)
Solving nonlinear problems with local optimal solutions is performed using _____________, in Excel Solver, which is based on more classical optimization techniques.
(Multiple Choice)
5.0/5  (33)
(33)
In reviewing the image below, what is the minimum value for this function? 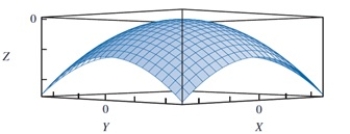
(Multiple Choice)
4.8/5  (38)
(38)
A function that is bowl-shaped down is called a ___________ function.
(Multiple Choice)
4.8/5  (35)
(35)
Develop a model that minimizes semivariance for the data given below with a required return of 15 percent. Define a variable for each scenario and let with = 0. Then make the objective function: Min . Scenario Mutual Fund Year 1 Year 2 Year 3 Year 4 Large-Cap Growth 41.54 36.18 32.76 -20.63 Large-Cap Value 32.45 44.78 28.61 38.49 Small-Cap Growth 26.13 7.04 -23.97 45.67 Small-Cap Value 37.56 18.53 27.53 -5.48 Solve the model you developed with a required expected return of at least 15 percent.
(Essay)
4.9/5  (36)
(36)
Consider the following data on the returns from bonds. Y ear Bon d 1 0.200 0.026 0.121 -0.139 -0.167 0.135 0.152 Bon d 2 0.128 0.100 0.125 -0.243 0.269 0.225 0.204 Bon d 3 0.067 0.700 0.226 -0.184 0.234 -0.146 0.047 Develop and solve the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur. Use this model to construct an efficient frontier by varying the expected return from 2 to 18 percent in increment of 2 percent and solving for the variance. Round all your answers to three decimal places.
(Essay)
4.9/5  (32)
(32)
Showing 41 - 55 of 55
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)