Exam 13: Nonlinear Optimization Models
Exam 1: Introduction49 Questions
Exam 2: Descriptive Statistics84 Questions
Exam 3: Data Visualization69 Questions
Exam 4: Descriptive Data Mining56 Questions
Exam 5: Probability: an Introduction to Modeling Uncertainty62 Questions
Exam 6: Statistical Inference62 Questions
Exam 7: Linear Regression71 Questions
Exam 8: Time Series Analysis and Forecasting58 Questions
Exam 9: Predictive Data Mining40 Questions
Exam 10: Spreadsheet Models64 Questions
Exam 11: Linear Optimization Models58 Questions
Exam 12: Integer Linear Optimization Models56 Questions
Exam 13: Nonlinear Optimization Models55 Questions
Exam 14: Monte Carlo Simulation59 Questions
Exam 15: Decision Analysis58 Questions
Select questions type
A function that is bowl-shaped up is called a(n) _________ function.
(Multiple Choice)
4.7/5  (34)
(34)
Jeff is willing to invest $5000 in buying shares and bonds of a company to gain maximum returns. From his past experience, he estimates the relationship between returns and investments made in this company to be:
R = -2S2 - 9B2 - 4SB + 20S + 30B.
where,
R = total returns in thousands of dollars
S = thousands of dollars spent on Shares
B = thousands of dollars spent on Bond
Jeff would like to develop a strategy that will lead to maximum return subject to the restriction provided on amount available for investment.
a. What is the value of return if $3,000 is invested in shares and $2,000 is invested bonds of the company?
b. Formulate an optimization problem that can be solved to maximize the returns subject to investing no more than $5,000 on both share and bonds.
c. Determine the optimal amount to invest in shares and bonds of the company. How much return will Jeff gain? Round all your answers to two decimal places.
(Essay)
4.8/5  (32)
(32)
Which of the following conclusions can be drawn from the below figure using the Bass forecasting model? (Note: Bass forecasting model is given by: Ft = (p + q[Ct - 1 /m]) (m - Ct - 1),
Where m = the number of people estimated to eventually adopt the new product,
Ct - 1 = the number of people who have adopted the product through time t - 1,
Q = the coefficient of imitation, and
P = the coefficient of innovation.) ![Which of the following conclusions can be drawn from the below figure using the Bass forecasting model? (Note: Bass forecasting model is given by: F<sub>t</sub> = (p + q[Ct<sub> - 1</sub> /m]) (m - Ct<sub> - 1</sub>), Where m = the number of people estimated to eventually adopt the new product, Ct<sub> - 1</sub> = the number of people who have adopted the product through time t - 1, Q = the coefficient of imitation, and P = the coefficient of innovation.)](https://storage.examlex.com/TB2760/11eb0ecc_0968_4ed0_9431_3722522061cb_TB2760_00.jpg)
(Multiple Choice)
4.9/5  (40)
(40)
An Electrical Company has two manufacturing plants. The cost in dollars of producing an Amplifier at each of the two plants is given below. The cost of producing Q1 Amplifiers at first plant is:
65Q1 + 4Q12+ 90
and the cost of producing Q2 Amplifiers at the second plant is
20Q2 + 2Q22+ 120
The company needs to manufacture at least 60 Amplifiers to meet the received orders. How many Amplifiers should be produced at each of the plant to minimize the total production cost? Round the answers to two decimal places and the total cost to the nearest dollar value.
(Essay)
4.8/5  (37)
(37)
In the Bass forecasting model, the __________ measures the likelihood of adoption due to a potential adopter being influenced by someone who has already adopted the product.
(Multiple Choice)
4.7/5  (33)
(33)
Mark and his friends are planning for a holiday party. Data on longitude, latitude, and number of friends at each of the 10 locations are given below. Mark would like to identify the location for the holiday party such that it minimizes the demand-weighted distance, where demand is the number of friends at each location. Find the optimal location for the party. The distance between two cities can be approximated by the following formula. where lat1 and long1 are the latitude and longitude of city 1, and lat2 and long2 are the latitude and longitude of city 2. (Hint: Notice that all longitude values given for this problem are negative. Make sure that you do not check the option for Make Unconstrained Variables Non-Negative in Solver.) Location latitude longitude Friends Ohio 26.782 -77.639 12 TN 38.952 -76.164 2 Mass 36.961 -85.921 1 Iowa 33.216 -81.753 8 New York 36.499 -84.575 10 Virginia 44.934 -72.798 7 NJ 40.850 -76.657 5 Wyoming 42.901 -75.514 6 Maryland 41.019 -120.491 1 CA 43.623 -119.626 9
(Essay)
4.9/5  (30)
(30)
In a nonlinear problem, the rate of change of the objective function with respect to the right-hand side of a constraint is given by the
(Multiple Choice)
4.8/5  (29)
(29)
Consider the stock return data given below. Stock Month 1 Month 2 Month 3 Month 4 Month 5 A 12.07 10.12 14.54 46.58 -19.34 B 15.95 4.16 6.31 -2.74 6.54 C 30.52 16.51 34.25 45.62 -27.21 D 32.42 21.36 13.84 8.12 -6.84
a. Construct the Markowitz model that maximizes expected return subject to a maximum variance of 35.
a. Round all your answers to three decimal places.
b. Solve the model developed in part
(Essay)
4.8/5  (33)
(33)
A feasible solution is ____________ if there are no other feasible points with a smaller objective function value in the entire feasible region.
(Multiple Choice)
4.9/5  (42)
(42)
Using the graph below, the feasible region for the function represented in the graph is 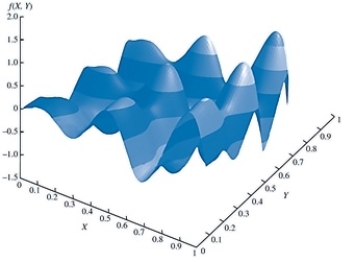
(Multiple Choice)
4.8/5  (33)
(33)
In reviewing the image below, the point (0, 0, 0) is a(n) __________ for the given concave function. 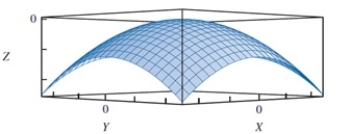
(Multiple Choice)
4.7/5  (29)
(29)
If there are no other feasible points with a larger objective function value in the entire feasible region, a feasible solution is
(Multiple Choice)
4.8/5  (37)
(37)
A feasible solution is a(n) ___________ if there are no other feasible solutions with a better objective function value in the immediate neighborhood.
(Multiple Choice)
4.9/5  (28)
(28)
A portfolio optimization model used to construct a portfolio that minimizes risk subject to a constraint requiring a minimum level of return is known as
(Multiple Choice)
4.8/5  (34)
(34)
Gatson manufacturing company is willing to promote 2 types of tires: Economy tire and Premium tire. These two tires are independent of each other in terms of demand, cost, price, etc. An analytics team of this company has estimated the profit functions for both the tires as
Monthly profit for Economy tire = 49.2415 IN(XA) + 180.414
Monthly profit for Premium tire = 84.344 IN(XB) - 150.112
where XA and XB are the advertising amount allocated to Economy tire and Premium tire, respectively, and IN is the natural logarithm function. The advertising budget is $200,000, and management has dictated that at least $20,000 must be allocated to each of the two tires.
(Hint: To compute a natural logarithm for the value X in Excel, use the formula = IN(X). For Solver to find an answer, you also need to start with decision variable values greater than 0 in this problem.)
Develop and solve an optimization model that will prescribe how the company should allocate its marketing budget to maximize profit.
(Essay)
4.9/5  (29)
(29)
In reviewing the image below, which of the following functions is most likely to yield the above shape? 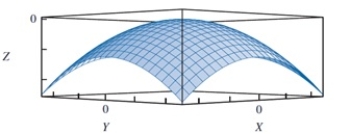
(Multiple Choice)
4.7/5  (29)
(29)
The measure of risk most often associated with the Markowitz portfolio model is the
(Multiple Choice)
4.8/5  (31)
(31)
Roger is willing to promote and sell two types of smart watches, X and Y, at his outlet. The demand for these two watches are as follows.
DX = -0.45PX + 0.34PY + 242
DY = 0.2PX - 0.58PY+ 282
where, DX is the demand for watch X, PX is the selling price of watch X, DY is the demand for watch Y, and PY is the selling price of watch Y.
Rogers wishes to determine the selling price that maximizes revenue for these two products. Develop the revenue function for these two models, and find the revenue maximizing prices.
(Essay)
4.7/5  (30)
(30)
Showing 21 - 40 of 55
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)