Exam 2: An Introduction to Linear Programming
Exam 1: Introduction49 Questions
Exam 2: An Introduction to Linear Programming52 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution47 Questions
Exam 4: Linear Programming Applications in Marketing, Finance and Operations Management38 Questions
Exam 5: Advanced Linear Programming Applications35 Questions
Exam 6: Distribution and Network Problems54 Questions
Exam 7: Integer Linear Programming43 Questions
Exam 8: Nonlinear Optimization Models48 Questions
Exam 9: Project Scheduling: Pertcpm44 Questions
Exam 10: Inventory Models51 Questions
Exam 11: Waiting Line Models48 Questions
Exam 12: Simulation49 Questions
Exam 13: Decision Analysis42 Questions
Exam 14: Multicriteria Decisions45 Questions
Exam 15: Forecasting47 Questions
Exam 16: Markov Processes41 Questions
Exam 17: Linear Programming: Simplex Method46 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality34 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems42 Questions
Exam 20: Minimal Spanning Tree18 Questions
Exam 21: Dynamic Programming30 Questions
Select questions type
Maxwell Manufacturing makes two models of felt tip marking pens. Requirements for each lot of pens are given below. Fliptop Model Tiptop Model Available Plastic 3 4 36 Ink Assembly 5 4 40 Molding Time 5 2 30 The profit for either model is $1000 per lot.
a.What is the linear programming model for this problem?
b.Find the optimal solution.
c.Will there be excess capacity in any resource?
Free
(Essay)
4.8/5  (36)
(36)
Correct Answer:
a.Let F = the number of lots of Fliptip pens to produce
Let T = the number of lots of Tiptop pens to produce
Max
1000F + 1000T
s.t.3F + 4T 36
5F + 4T 40
5F + 2T 30
F , T 0
b. 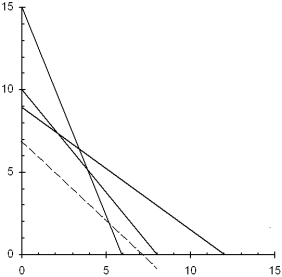 The complete optimal solution is F = 2, T = 7.5, Z = 9500, S1 = 0, S2 = 0, S3 = 5
The complete optimal solution is F = 2, T = 7.5, Z = 9500, S1 = 0, S2 = 0, S3 = 5
c.There is an excess of 5 units of molding time available.
Decision variables limit the degree to which the objective in a linear programming problem is satisfied.
Free
(True/False)
4.8/5  (36)
(36)
Correct Answer:
False
For the following linear programming problem, determine the optimal solution by the graphical solution method. Are any of the constraints redundant? If yes, then identify the constraint that is redundant.
Max
X + 2Y
s.t.
X + Y 3
X- 2Y 0
Y 1
X , Y 0
(Essay)
4.8/5  (38)
(38)
No matter what value it has, each objective function line is parallel to every other objective function line in a problem.
(True/False)
4.8/5  (37)
(37)
Because surplus variables represent the amount by which the solution exceeds a minimum target, they are given positive coefficients in the objective function.
(True/False)
4.8/5  (46)
(46)
The Sanders Garden Shop mixes two types of grass seed into a blend. Each type of grass has been rated (per pound) according to its shade tolerance, ability to stand up to traffic, and drought resistance, as shown in the table. Type A seed costs $1 and Type B seed costs $2. If the blend needs to score at least 300 points for shade tolerance, 400 points for traffic resistance, and 750 points for drought resistance, how many pounds of each seed should be in the blend? Which targets will be exceeded? How much will the blend cost? Type A Type B Shade Tolerance 1 1 Traffic Resistance 2 1 Drought Resistance 2 5
(Essay)
4.7/5  (34)
(34)
Whenever all the constraints in a linear program are expressed as equalities, the linear program is said to be written in
(Multiple Choice)
4.8/5  (24)
(24)
Explain what to look for in problems that are infeasible or unbounded.
(Essay)
4.8/5  (30)
(30)
In a feasible problem, an equal-to constraint cannot be nonbinding.
(True/False)
4.8/5  (34)
(34)
An optimal solution to a linear programming problem can be found at an extreme point of the feasible region for the problem.
(True/False)
4.8/5  (31)
(31)
Solve the following system of simultaneous equations.
6X + 2Y = 50
2X + 4Y = 20
(Short Answer)
4.9/5  (23)
(23)
The constraint 2x1 - x2 = 0 passes through the point (200, 100).
(True/False)
5.0/5  (38)
(38)
All linear programming problems have all of the following properties EXCEPT
(Multiple Choice)
4.9/5  (43)
(43)
Consider the following linear programming problem
Max
8X + 7Y
s.t.
15X + 5Y 75
10X + 6Y 60
X + Y 8
X , Y 0
a.Use a graph to show each constraint and the feasible region.
b.Identify the optimal solution point on your graph.What are the values of X and Y at the optimal solution?
c.What is the optimal value of the objective function?
(Essay)
4.8/5  (30)
(30)
Showing 1 - 20 of 52
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)