Exam 2: An Introduction to Linear Programming

Use this graph to answer the questions. 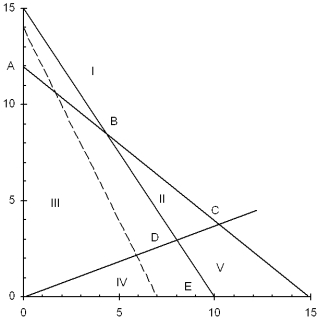Max 20X + 10Y s.t. 12X + 15Y $\le$ 180 15X + 10Y $\le$ 150 3X - 8Y $\le$ 0 X , Y $\ge$ 0 a.Which area (I, II, III, IV, or V) forms the feasible region? b.Which point (A, B, C, D, or E) is optimal? c.Which constraints are binding? d.Which slack variables are zero?

Does the following linear programming problem exhibit infeasibility, unboundedness, or alternate optimal solutions? Explain. Min 3X + 3Y s.t. 1X + 2Y $\le$ 16 1X + 1Y $\le$ 10 5X + 3Y $\le$ 45 X , Y $\ge$ 0

A range of optimality is applicable only if the other coefficient remains at its original value.

Alternative optimal solutions occur when there is no feasible solution to the problem.

Muir Manufacturing produces two popular grades of commercial carpeting among its many other products. In the coming production period, Muir needs to decide how many rolls of each grade should be produced in order to maximize profit. Each roll of Grade X carpet uses 50 units of synthetic fiber, requires 25 hours of production time, and needs 20 units of foam backing. Each roll of Grade Y carpet uses 40 units of synthetic fiber, requires 28 hours of production time, and needs 15 units of foam backing. The profit per roll of Grade X carpet is $200 and the profit per roll of Grade Y carpet is $160. In the coming production period, Muir has 3000 units of synthetic fiber available for use. Workers have been scheduled to provide at least 1800 hours of production time (overtime is a possibility). The company has 1500 units of foam backing available for use. Develop and solve a linear programming model for this problem.

Which of the following special cases does not require reformulation of the problem in order to obtain a solution?

In a linear programming problem, the objective function and the constraints must be linear functions of the decision variables.

To find the optimal solution to a linear programming problem using the graphical method

Which of the following is a valid objective function for a linear programming problem?

Because the dual price represents the improvement in the value of the optimal solution per unit increase in right-hand side, a dual price cannot be negative.

As long as the slope of the objective function stays between the slopes of the binding constraints

The maximization or minimization of a quantity is the

Only binding constraints form the shape (boundaries) of the feasible region.

A businessman is considering opening a small specialized trucking firm. To make the firm profitable, it is estimated that it must have a daily trucking capacity of at least 84,000 cu. ft. Two types of trucks are appropriate for the specialized operation. Their characteristics and costs are summarized in the table below. Note that truck 2 requires 3 drivers for long haul trips. There are 41 potential drivers available and there are facilities for at most 40 trucks. The businessman's objective is to minimize the total cost outlay for trucks. Capacity Drivers Truck Cost (.) Needed Small \ 18,000 2,400 1 Large \ 45,000 6,000 3 Solve the problem graphically and note there are alternate optimal solutions. Which optimal solution: a.uses only one type of truck? b.utilizes the minimum total number of trucks? c.uses the same number of small and large trucks?

Create a linear programming problem with two decision variables and three constraints that will include both a slack and a surplus variable in standard form. Write your problem in standard form.

The improvement in the value of the objective function per unit increase in a right-hand side is the

Increasing the right-hand side of a nonbinding constraint will not cause a change in the optimal solution.

Explain the concepts of proportionality, additivity, and divisibility.

Find the complete optimal solution to this linear programming problem. Max 2X + 3Y s.t. 4X + 9Y $\le$ 72 10X + 11Y $\le$ 110 17X + 9Y $\le$ 153 X , Y $\ge$ 0

Find the complete optimal solution to this linear programming problem. Min 3X + 3Y s.t. 12X + 4Y $\ge$ 48 10X + 5Y $\ge$ 50 4X + 8Y $\ge$ 32 X , Y $\ge$ 0