Exam 14: Simple Linear Regression
Exam 1: Data and Statistics84 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays67 Questions
Exam 3: Descriptive Statistics: Numerical Measures127 Questions
Exam 4: Introduction to Probability99 Questions
Exam 5: Discrete Probability Distributions86 Questions
Exam 6: Continuous Probability Distributions120 Questions
Exam 7: Sampling and Sampling Distributions117 Questions
Exam 8: Interval Estimation144 Questions
Exam 9: Hypothesis Tests129 Questions
Exam 10: Inference About Means and Proportions With Two Populations85 Questions
Exam 11: Inferences About Population Variances85 Questions
Exam 12: Comparing Multiple Proportions, Tests of Independence and Goodness of Fit59 Questions
Exam 13: Experimental Design and Analysis of Variance80 Questions
Exam 14: Simple Linear Regression131 Questions
Exam 15: Multiple Regression103 Questions
Select questions type
The following information regarding a dependent variable (y) and an independent variable (x) is provided.  SSE = 1.9
SST = 6.8
The MSE is
SSE = 1.9
SST = 6.8
The MSE is
(Multiple Choice)
4.8/5  (37)
(37)
Given the following regression source table, can we say that the slope is significant at 5%?
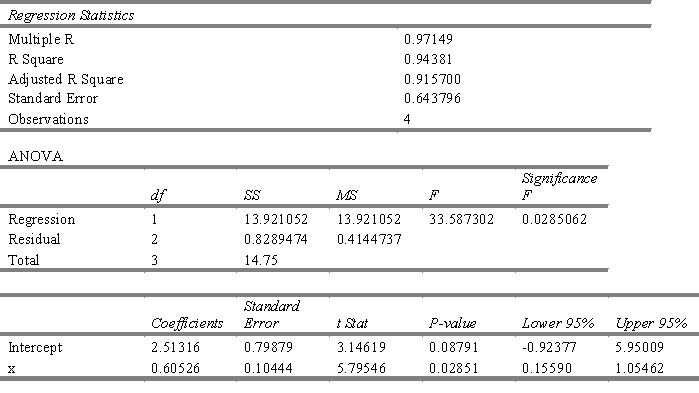
(Essay)
4.8/5  (33)
(33)
In a regression analysis, the regression equation is given by y = 12 - 6x.If SSE = 510 and SST = 1000, then the coefficient of correlation is
(Multiple Choice)
4.9/5  (40)
(40)
The following information regarding a dependent variable (y) and an independent variable (x) is provided.  SSE = 1.9
SST = 6.8
The coefficient of determination is
SSE = 1.9
SST = 6.8
The coefficient of determination is
(Multiple Choice)
4.9/5  (38)
(38)
The proportion of the variation in the dependent variable y that is explained by the estimated regression equation is measured by the
(Multiple Choice)
4.8/5  (36)
(36)
The interval estimate of the mean value of y for a given value of x is the
(Multiple Choice)
4.9/5  (30)
(30)
You are given the following information about y and x.  The least squares estimate of the intercept or b0 equals
The least squares estimate of the intercept or b0 equals
(Multiple Choice)
4.9/5  (44)
(44)
Application of the least squares method results in values of the y-intercept and the slope that minimizes the sum of the squared deviations between the
(Multiple Choice)
4.8/5  (33)
(33)
The following information regarding a dependent variable y and an independent variable x is provided:  The sum of squares due to error (SSE) is
The sum of squares due to error (SSE) is
(Multiple Choice)
4.8/5  (35)
(35)
If the coefficient of correlation is a negative value, then the coefficient of determination
(Multiple Choice)
4.8/5  (24)
(24)
A descriptive measure of the strength of linear association between two variables is the
(Multiple Choice)
4.9/5  (37)
(37)
You are given the following information about y and x.  The sample correlation coefficient equals
The sample correlation coefficient equals
(Multiple Choice)
4.8/5  (38)
(38)
If the coefficient of determination is equal to 1, then the coefficient of correlation
(Multiple Choice)
4.8/5  (39)
(39)
The equation that describes how the dependent variable (y) is related to the independent variable (x) is called
(Multiple Choice)
4.8/5  (41)
(41)
You are given the following information about y and x.  The least squares estimate of the slope or b1 equals
The least squares estimate of the slope or b1 equals
(Multiple Choice)
4.8/5  (39)
(39)
A regression analysis between sales (in $1000) and price (in dollars) resulted in the following equation: 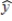 = 40 - 6x
The above equation implies that an
= 40 - 6x
The above equation implies that an
(Multiple Choice)
4.8/5  (36)
(36)
In regression analysis, which of the following assumptions is not true about the error term ε?
(Multiple Choice)
4.8/5  (35)
(35)
If a data set produces SST =1000 and SSE =600, then the coefficient of determination is
(Multiple Choice)
4.8/5  (25)
(25)
Showing 101 - 120 of 131
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)