Exam 13: Experimental Design and Analysis of Variance
Exam 1: Data and Statistics84 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays67 Questions
Exam 3: Descriptive Statistics: Numerical Measures127 Questions
Exam 4: Introduction to Probability99 Questions
Exam 5: Discrete Probability Distributions86 Questions
Exam 6: Continuous Probability Distributions120 Questions
Exam 7: Sampling and Sampling Distributions117 Questions
Exam 8: Interval Estimation144 Questions
Exam 9: Hypothesis Tests129 Questions
Exam 10: Inference About Means and Proportions With Two Populations85 Questions
Exam 11: Inferences About Population Variances85 Questions
Exam 12: Comparing Multiple Proportions, Tests of Independence and Goodness of Fit59 Questions
Exam 13: Experimental Design and Analysis of Variance80 Questions
Exam 14: Simple Linear Regression131 Questions
Exam 15: Multiple Regression103 Questions
Select questions type
Part of an ANOVA table is shown below.  The number of degrees of freedom corresponding to between-treatments is
The number of degrees of freedom corresponding to between-treatments is
(Multiple Choice)
4.8/5  (37)
(37)
In factorial designs, the response produced when the treatments of one factor interact with the treatments of another in influencing the response variable is known as
(Multiple Choice)
4.8/5  (32)
(32)
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations).Also, the design provided the following information.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The number of degrees of freedom corresponding to within-treatments is
(Multiple Choice)
4.8/5  (33)
(33)
Consider the following information. 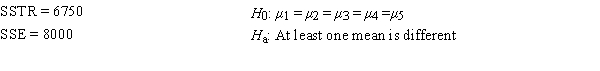
The null hypothesis is to be tested at the 5% level of significance.The null hypothesis
The null hypothesis is to be tested at the 5% level of significance.The null hypothesis
(Multiple Choice)
4.8/5  (34)
(34)
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below. 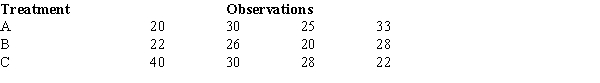
The test statistic to test the null hypothesis equals
The test statistic to test the null hypothesis equals
(Multiple Choice)
4.8/5  (47)
(47)
Consider the following ANOVA table. 
The sum of squares due to error equals
The sum of squares due to error equals
(Multiple Choice)
4.8/5  (34)
(34)
MNM, Inc.has three stores located in three different areas.Random samples of the daily sales of the three stores (in $1000) are shown below. 
At the 1% level of significance, test to see if there is a significant difference in the average sales of the three stores.Use both the critical and p-value approaches.
At the 1% level of significance, test to see if there is a significant difference in the average sales of the three stores.Use both the critical and p-value approaches.
(Essay)
4.8/5  (34)
(34)
Part of an ANOVA table is shown below.  The mean square due to error (MSE) is
The mean square due to error (MSE) is
(Multiple Choice)
4.8/5  (35)
(35)
Which of the following is not a required assumption for the analysis of variance?
(Multiple Choice)
4.9/5  (33)
(33)
Part of an ANOVA table is shown below.  If we want to determine whether or not the means of the populations are equal, the p-value is
If we want to determine whether or not the means of the populations are equal, the p-value is
(Multiple Choice)
4.9/5  (39)
(39)
Part of an ANOVA table is shown below.  The mean square due to treatments (MSTR) is
The mean square due to treatments (MSTR) is
(Multiple Choice)
4.7/5  (33)
(33)
In an ANOVA procedure, a term that means the same as the term "variable" is
(Multiple Choice)
4.7/5  (43)
(43)
The marketing department of a company has designed three different packing boxes for its product.It wants to determine which box will produce the largest amount of sales.Each box will be test-marketed in five different stores for a period of a month.Below you are given the information on sales (in dollars). 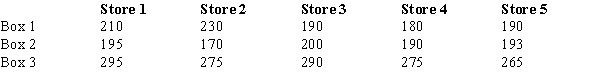
a.
State the null and alternative hypotheses.
b.
Construct an ANOVA table.
c.
What conclusion do you draw?
d.
Use Fisher's LSD procedure and determine which mean (if any) is different from the others.Let α = .01.
a.
State the null and alternative hypotheses.
b.
Construct an ANOVA table.
c.
What conclusion do you draw?
d.
Use Fisher's LSD procedure and determine which mean (if any) is different from the others.Let α = .01.
(Essay)
4.7/5  (33)
(33)
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below. 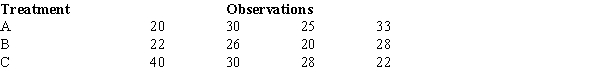 The mean square due to error (MSE) equals
The mean square due to error (MSE) equals
(Multiple Choice)
4.9/5  (32)
(32)
Consider the following information. 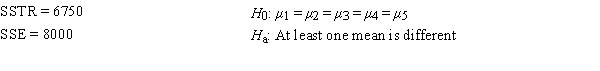
The test statistic to test the null hypothesis equals
The test statistic to test the null hypothesis equals
(Multiple Choice)
4.7/5  (31)
(31)
Six observations were selected from each of three populations.The data obtained is shown below. 
Test at the .05 level to determine if there is a significant difference in the means of the three populations.Use both the critical value and the p-value approaches.
Test at the .05 level to determine if there is a significant difference in the means of the three populations.Use both the critical value and the p-value approaches.
(Essay)
4.8/5  (25)
(25)
The ANOVA procedure is a statistical approach for determining whether or not the means of _____ are equal.
(Multiple Choice)
4.8/5  (20)
(20)
Part of an ANOVA table is shown below.  The test statistic is
The test statistic is
(Multiple Choice)
4.8/5  (40)
(40)
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below. 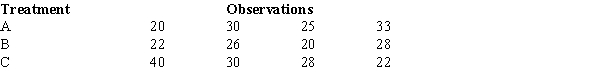
The null hypothesis is to be tested at the 1% level of significance.The p-value is
The null hypothesis is to be tested at the 1% level of significance.The p-value is
(Multiple Choice)
4.8/5  (39)
(39)
An ANOVA procedure is used for data that was obtained from five sample groups each comprised of six observations.The degrees of freedom for the critical value of F are
(Multiple Choice)
4.8/5  (32)
(32)
Showing 41 - 60 of 80
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)