Exam 6: Normal Probability Distributions
Exam 1: Introduction to Statistics59 Questions
Exam 2: Exploring Data With Tables and Graphs59 Questions
Exam 3: Describing, Exploring, and Comparing Data59 Questions
Exam 4: Probability60 Questions
Exam 5: Discrete Probability Distributions59 Questions
Exam 6: Normal Probability Distributions60 Questions
Exam 7: Estimating Parameters and Determining Sample Sizes58 Questions
Exam 8: Hypothesis Testing57 Questions
Exam 9: Inferences From Two Samples58 Questions
Exam 10: Correlation and Regression56 Questions
Exam 11: Chi-Square and Analysis of Variance60 Questions
Exam 12: Statistical Control Charts, Nonparametric Tests, and Hypothesis Testing181 Questions
Select questions type
An unbiased estimator is a statistic that targets the value of the of the population parameter such that the sampling distribution of the statistic has a __________equal to the _________ of
The corresponding parameter.
(Multiple Choice)
4.8/5  (41)
(41)
If z is a standard normal variable, find the probability: P(-0.73<z<2.27)
(Multiple Choice)
4.8/5  (35)
(35)
In one region, the September energy consumption levels for single -family homes are found to be normally distributed with a mean of 1050 kWh and a standard deviation of 218 kWh. For a
Randomly selected home, find the probability that the September energy consumption level is
Between 1100 kWh and 1225 kWh.
(Multiple Choice)
4.9/5  (38)
(38)
The population of current statistics students has ages with mean and standard deviation Samples of statistics are randomly selected so that there are exactly 40 students in each sample. For each sample, the mean age is computed. What does the central limit theorem tell us about the distribution of those mean ages?
(Essay)
4.9/5  (42)
(42)
The Precision Scientific Instrument Company manufactures thermometers that are supposed to give readings of 0°C at the freezing point of water. Tests on a large sample of these
Thermometers reveal that at the freezing point of water, some give readings below 0°C
(denoted by negative numbers)and some give readings above 0°C (denoted by positive
Numbers). Assume that the mean reading is 0°C and the standard deviation of the readings is
1.00°C. Also assume that the frequency distribution of errors closely resembles the normal
Distribution. A thermometer is randomly selected and tested. A quality control analyst wants
To examine thermometers that give readings in the bottom 4%. Find the temperature reading
That separates the bottom 4% from the others.
(Multiple Choice)
4.9/5  (32)
(32)
A study of the amount of time it takes a mechanic to rebuild the transmission for a 2010 Chevrolet Colorado shows that the mean is 8.4 hours and the standard deviation is 1.8 hours.
If 40 mechanics are randomly selected, find the probability that their mean rebuild time is less
Than 8.9 hours.
(Multiple Choice)
4.8/5  (35)
(35)
The probability that a radish seed will germinate is 0.7. Estimate the probability that of 140 randomly selected seeds, exactly 100 will germinate.
(Multiple Choice)
4.9/5  (31)
(31)
A normal quartile plot is given below for the weekly incomes (in dollars)of a sample of
engineers in one town. Describe what each x value represents and what each y value
represents. Use the plot to assess the normality of the incomes of engineers in this town.
Explain your reasoning. 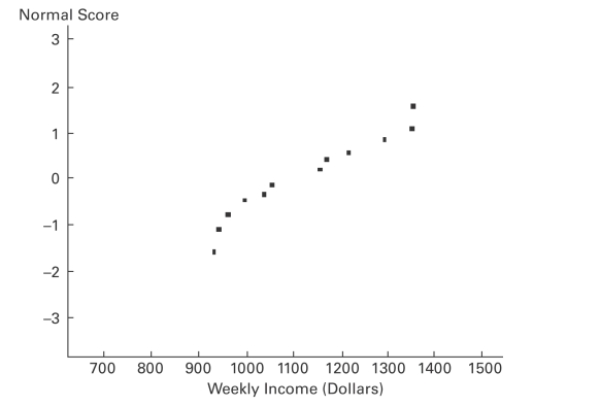
(Essay)
4.7/5  (42)
(42)
Assume that the weight loss for the first month of a diet program varies between 6 pounds and 12 pounds, and is spread evenly over the range of possibilities, so that there is a uniform distribution. Find the probability that the given range of pounds lost is between 8 pounds and 11 pounds.
(Multiple Choice)
4.8/5  (28)
(28)
The number of books sold over the course of the four-day book fair were 194, 197, 247, and
76. Assume that samples of size 2 are randomly selected with replacement from this
population of four values. List the different possible samples, and find the mean of each of
them.
(Essay)
4.9/5  (33)
(33)
In a population of 210 women, the heights of the women are normally distributed with a mean of 64.4 inches and a standard deviation of 2.9 inches. If 36 women are selected at random, find the mean and standard deviation of the population of sample means. Assume that the sampling is done without replacement and use a finite population correction factor.
(Multiple Choice)
4.8/5  (35)
(35)
Using the following uniform density curve, answer the question. 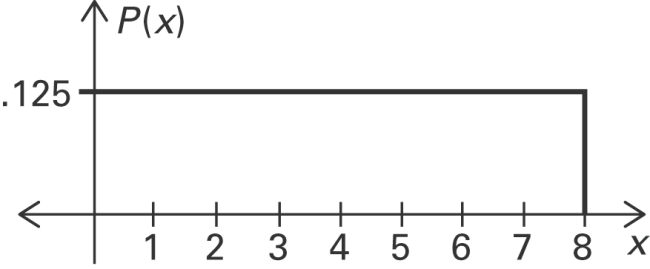 What is the probability that the random variable has a value greater than 5?
What is the probability that the random variable has a value greater than 5?
(Multiple Choice)
4.7/5  (37)
(37)
Assume that the red blood cell counts of women are normally distributed with a mean of 4.577 million cells per microliter and a standard deviation of 0.382 million cells per
Microliter. Find the 80th percentile for the red blood cell counts of women.
(Multiple Choice)
4.9/5  (31)
(31)
The weights of college football players are normally distributed with a mean of 200 pounds and a standard deviation of 50 pounds. If a college football player is randomly selected, find
The probability that he weighs between 170 and 220 pounds.
(Multiple Choice)
4.9/5  (41)
(41)
A coin is tossed 20 times. A person who claims to have extrasensory perception is asked to predict the outcome of each flip in advance. She predicts correctly on 14 tosses. What is the
Probability of being correct 14 or more times by guessing? Does this probability seem to
Verify her claim? Use the normal distribution to approximate the desired probability.
(Multiple Choice)
4.8/5  (32)
(32)
Heights of adult females are normally distributed. Samples of height of adult females, each of
size n = 3, are randomly collected and the sample means are found. Is it correct to conclude
that the sample means cannot be treated as a normal distribution because the sample size is so
small? Explain.
(Essay)
4.7/5  (37)
(37)
Lengths of pregnancies are normally distributed with a mean of 268 days and a standard
deviation of 15 days. (a)Find the probability of a pregnancy lasting more than 250 days.
(b)Find the probability of a pregnancy lasting more than 280 days. Draw the diagram for
each and discuss the part of the solution that would be different for finding the requested
probabilities.
(Essay)
4.9/5  (40)
(40)
Estimate the indicated probability by using the normal distribution as an approximation to the binomial distribution. Two percent of hair dryers produced in a certain plant are
Defective. Estimate the probability that of 10,000 randomly selected hair dryers, at least 219
Are defective.
(Multiple Choice)
4.9/5  (39)
(39)
In a recent year, the U.S. Mint in Denver manufactured 270 million quarters. Assume that on
each day of production, a sample of 50 quarters is randomly selected and the mean weight is
obtained. Given that the population of quarters has a mean weight of 5.67 g, what do you
know about the mean of the sample means? What do you know about the shape of the
distribution of the sample means?
(Essay)
4.7/5  (36)
(36)
Showing 41 - 60 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)