Exam 10: Hypothesis Tests Regarding a Parameter
Exam 1: Data Collection113 Questions
Exam 2: Organizing and Summarizing Data82 Questions
Exam 3: Numerically Summarizing Data141 Questions
Exam 4: Describing the Relation Between Two Variables72 Questions
Exam 5: Probability257 Questions
Exam 6: Discrete Probability Distributions131 Questions
Exam 7: The Normal Probability Distribution120 Questions
Exam 8: Sampling Distributions52 Questions
Exam 9: Estimating the Value of a Parameter88 Questions
Exam 10: Hypothesis Tests Regarding a Parameter140 Questions
Exam 11: Inferences on Two Samples129 Questions
Exam 12: Inference on Categorical Data38 Questions
Exam 13: Comparing Three or More Means51 Questions
Select questions type
Test the claim that Assume that the population is normally distributed.
(Essay)
4.8/5  (29)
(29)
Use a t-test to test the claim μ < 12.6 at α = 0.10, given the sample statistics Round the test statistic to the nearest thousandth.
(Essay)
4.9/5  (37)
(37)
Use a t-test to test the claim μ ≥ 9.7 at α = 0.05, given the sample statistics Round the test statistic to the nearest thousandth .
(Essay)
4.9/5  (30)
(30)
It is desired to test against using . The population in question is uniformly distributed with a standard deviation of 10 . A random sample of 36 will be drawn from this population. If is really equal to 35 , what is the probability that the hypothesis test would lead the investigator to commit a Type II error?
(Multiple Choice)
4.8/5  (36)
(36)
A relative frequency histogram for the sale prices of homes sold in one city during 2010 is shown below. Basedon the histogram, is a large sample necessary to conduct a hypothesis test about the mean sale price? If so,why? 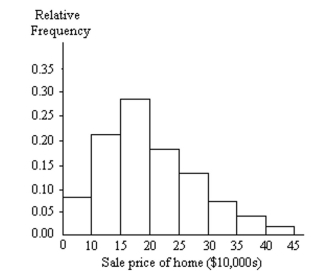
(Multiple Choice)
4.8/5  (31)
(31)
Determine the critical value for a right-tailed test of a population standard deviation with 22 degrees offreedom at the α = 0.05 level of significance.
(Multiple Choice)
4.8/5  (25)
(25)
A coin is tossed 1000 times and 570 heads appear. At α = 0.05, test the claim that this is not a biased coin.
(Essay)
4.9/5  (39)
(39)
The mean age of judges in Los Angeles is 48.6 years. Identify the type I and type II errors for the hypothesis testof this claim.
(Essay)
4.8/5  (37)
(37)
Determine the critical value for a right-tailed test of a population mean at the α = 0.001 level of significancewith 15 degrees of freedom.
(Multiple Choice)
4.7/5  (34)
(34)
A candidate for state representative of a certain state claims to be favored by at least half of the voters. If ahypothesis test is performed, how should you interpret a decision that fails to reject the null hypothesis?
(Multiple Choice)
4.8/5  (37)
(37)
A survey claims that 9 out of 10 doctors (i.e., 90 % ) recommend brand Z for their patients who have children. To test this claim against the alternative that the actual proportion of doctors who recommend brand Z is less than 90 % , a random sample of doctors was taken. Suppose the test statistic is z= -2.23 . Can we conclude that H0 should be rejected at the a) level?
(Multiple Choice)
4.8/5  (32)
(32)
If we do not reject the null hypothesis when the null hypothesis is in error, then we have made a
(Multiple Choice)
4.8/5  (38)
(38)
A new gun-like apparatus has been devised to replace the needle in administering vaccines. The apparatus,which is connected to a large supply of vaccine, can be set to inject different amounts of the serum, but thevariance in the amount of serum injected to a given person must not be greater than 0.0 8 to ensure properinoculation. A random sample of 25 injections was measured. Suppose the P-value for the test is p = 0.0085.State the proper conclusion using α = 0.01.10.5 Putting It Together: Which Method Do I Use?1 Determine the appropriate hypothesis test to perform.
(Essay)
4.9/5  (32)
(32)
We never conclude "Accept H0 " in a test of hypothesis. This is because:
(Multiple Choice)
4.8/5  (35)
(35)
Use a t-test to test the claim μ = 10 at α = 0.01given the sample statistics . Round the test statistic to the nearest thousandth.
(Essay)
4.7/5  (32)
(32)
Use a t-test to test the claim μ ≤ 8.9 at α = 0.05, given the sample statistics Round the test statistic to he nearest thousandth .
(Essay)
4.9/5  (34)
(34)
Find the standardized test statistic t for a sample with your answer to three decimal places.
(Multiple Choice)
4.7/5  (35)
(35)
Compute the standardized test statistic, to test the claim
(Multiple Choice)
4.8/5  (41)
(41)
A local tennis pro-shop strings tennis rackets at the tension (pounds per square inch) requested by thecustomer. Recently a customer made a claim that the pro-shop consistently strings rackets at lower tensions, onaverage, than requested. To support this claim, the customer asked the pro shop to string 12 new rackets at 53psi. Upon receiving the rackets, the customer measured the tension of each and calculated the followingsummary statistics: psi. In order to conduct the test, the customer selected a significance levelof α = .05. Interpret this value.
(Multiple Choice)
4.8/5  (31)
(31)
Showing 121 - 140 of 140
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)