Question 1

Determine all possible rational solutions of the polynomial equation.
-$$f ( x ) = 6 x ^ { 3 } + 24 x ^ { 2 } + 2 x - 3$$

Accepted Answer

A)  $\pm 1 , \pm \frac { 1 } { 2 } , \pm 3 , \pm \frac { 3 } { 2 } , \pm \frac { 1 } { 3 } , \pm \frac { 1 } { 6 }$ 
B)  $\pm 1 , \pm \frac { 1 } { 2 } , \pm 3 , \pm \frac { 2 } { 3 } , \pm \frac { 1 } { 6 }$ 
C)  $\pm 1 , \pm \frac { 1 } { 3 } , \pm 2 , \pm \frac { 2 } { 3 } , \pm 3 , \pm 6$ 
D)  $\pm 1 , \pm 3 , \pm \frac { 1 } { 2 }$ 
A)  $\pm 1 , \pm \frac { 1 } { 2 } , \pm 3 , \pm \frac { 3 } { 2 } , \pm \frac { 1 } { 3 } , \pm \frac { 1 } { 6 }$ 
B)  $\pm 1 , \pm \frac { 1 } { 2 } , \pm 3 , \pm \frac { 2 } { 3 } , \pm \frac { 1 } { 6 }$ 
C)  $\pm 1 , \pm \frac { 1 } { 3 } , \pm 2 , \pm \frac { 2 } { 3 } , \pm 3 , \pm 6$ 
D)  $\pm 1 , \pm 3 , \pm \frac { 1 } { 2 }$

Question 2

The table below gives the number of births, in thousands, to females over the age of 35 for a particular state every two years from 1994 to 2010. $$\begin{array} { c | c } 
& \text { Births } \
\text { Year } & \text { (thousands) } \
\hline 1994 & 42.5 \
\hline 1996 & 29.9 \
\hline 1998 & 36.0 \
\hline 2000 & 56.9 \
\hline 2002 & 71.1 \
\hline 2004 & 69.9 \
\hline 2006 & 57.2 \
\hline 2008 & 37.1 \
\hline 2010 & 25.9
\end{array}$$ Use technology to find the quartic function that is the best fit for this data, where x is the number of years after 1994.
According to the model, when will the number of births to females over the age of 35 first reach 80,000?

Accepted Answer

A)  2015 
B)  2014 
C)  2016 
D)  2013 
A)  2015 
B)  2014 
C)  2016 
D)  2013

Question 3

State the degree and leading coefficient of the polynomial function.
-$$f ( x ) = - 8 + 10 x ^ { 4 } + 13 x - 3 x ^ { 3 } - 7 x ^ { 2 }$$

Accepted Answer

A)  Degree: $- 8$; leading coefficient: 10 
B)  Degree: 4 ; leading coefficient: $- 8$ 
C)  Degree: 4; leading coefficient: 10 
D)  Degree: 3 ; leading coefficient: $- 3$ 
A)  Degree: $- 8$; leading coefficient: 10 
B)  Degree: 4 ; leading coefficient: $- 8$ 
C)  Degree: 4; leading coefficient: 10 
D)  Degree: 3 ; leading coefficient: $- 3$

Question 4

The table below gives the number of births, in thousands, to females over the age of 35 for a particular state every two years from 1994 to 2010. $\begin{array} { c | c } 
& \text { Births } \
\text { Year } & \text { (thousands) } \
\hline 1994 & 42.5 \
\hline 1996 & 29.9 \
\hline 1998 & 36.0 \
\hline 2000 & 56.9 \
\hline 2002 & 71.1 \
\hline 2004 & 69.9 \
\hline 2006 & 57.2 \
\hline 2008 & 37.1 \
\hline 2010 & 25.9
\end{array}$
 Use technology to find the quartic function that is the best fit for this data, where x is the number of years after 1994.
Round to five decimal places.

Accepted Answer

A)  $y = 43.26566 x ^ { 4 } - 18.98367 x ^ { 3 } + 6.66654 x ^ { 2 } - 0.62258 x + 0.01723$ 
B)  $y = - 0.01723 x ^ { 4 } + 0.62258 x ^ { 3 } - 6.66654 x ^ { 2 } + 18.98367 x - 43.26566$ 
C)  $y = 0.02223 x ^ { 4 } - 0.82248 x ^ { 3 } + 8.66654 x ^ { 2 } - 15.98367 x + 41.96566$ 
D)  $y = 0.01723 x ^ { 4 } - 0.62258 x ^ { 3 } + 6.66654 x ^ { 2 } - 18.98367 x + 43.26566$ 
A)  $y = 43.26566 x ^ { 4 } - 18.98367 x ^ { 3 } + 6.66654 x ^ { 2 } - 0.62258 x + 0.01723$ 
B)  $y = - 0.01723 x ^ { 4 } + 0.62258 x ^ { 3 } - 6.66654 x ^ { 2 } + 18.98367 x - 43.26566$ 
C)  $y = 0.02223 x ^ { 4 } - 0.82248 x ^ { 3 } + 8.66654 x ^ { 2 } - 15.98367 x + 41.96566$ 
D)  $y = 0.01723 x ^ { 4 } - 0.62258 x ^ { 3 } + 6.66654 x ^ { 2 } - 18.98367 x + 43.26566$

Question 5

The table below gives the number of births, in thousands, to females over the age of 35 for a particular state every two years from 1994 to 2010. $$\begin{array} { c | c } 
& \text { Births } \
\text { Year } & \text { (thousands) } \
\hline 1994 & 42.5 \
\hline 1996 & 29.9 \
\hline 1998 & 36.0 \
\hline 2000 & 56.9 \
\hline 2002 & 71.1 \
\hline 2004 & 69.9 \
\hline 2006 & 57.2 \
\hline 2008 & 37.1 \
\hline 2010 & 25.9
\end{array}$$ Use technology to find the quartic function that is the best fit for this data, where x is the number of years after 1994.
According to the model, how many births were there to females over the age of 35 in this state in 2014?

Accepted Answer

A)  106,368 
B)  108,868 
C)  94,368 
D)  101,318 
A)  106,368 
B)  108,868 
C)  94,368 
D)  101,318

Question 6

If a parking ramp attendant can wait on 6 vehicles per minute, and vehicles are leaving the ramp at  x  vehicles per minute, then the average wait in minutes for a car trying to exit is given by $f ( x ) = \frac { 1 } { 6 - x }$. Solve the inequality $2 \leq \frac { 1 } { 6 - x } \leq 10$ to determine the exit rates  x  that would result in average wait times between 2 and 10 minutes.

Accepted Answer

A)  $x \geq 5.9 \text { or } x \leq 5.5$ 
B)  $0.7 \leq x \leq 3.5$ 
C)  $5.4 \leq x \leq 6.0$ 
D)  $5.5 \leq x \leq 5.9$ 
A)  $x \geq 5.9 \text { or } x \leq 5.5$ 
B)  $0.7 \leq x \leq 3.5$ 
C)  $5.4 \leq x \leq 6.0$ 
D)  $5.5 \leq x \leq 5.9$

Question 7

Use analytical methods to solve the equation.
-$$\frac { x + 1 } { 2 } = \frac { x + 2 } { 3 }$$

Accepted Answer

A)  3 
B)  $- 3$ 
C)  1 
D)  $- 1$ 
A)  3 
B)  $- 3$ 
C)  1 
D)  $- 1$

Question 8

Determine whether the given constant is a solution to the given polynomial equation.
-$- x ^ { 4 } + 5 x ^ { 2 } - x - 2 = 0 ; - 1$

Accepted Answer

A)  No 
B)  Yes 
A)  No 
B)  Yes

Question 9

After an injection, the amount of a medication A in the bloodstream decreases with time t, in hours. Suppose that under certain conditions A is given b $A ( t ) = \frac { A _ { 0 } } { t ^ { 2 } + 1 }$ , where Ao is the initial amount of the medication
Given. Assume that an initial amount of 25.0 cc is injected. According to this function, does the medication ever
Completely leave the bloodstream?

Accepted Answer

A)  No 
B)  Yes 
A)  No 
B)  Yes

Question 10

Use the graph of f(x) to solve the inequality.
-$f(x)>0$

Accepted Answer

A)  $x  0$ 
C)  $- 1.7 < x < 1.7$ 
D)  $x \geq 0$ 
A)  $x  0$ 
C)  $- 1.7 < x < 1.7$ 
D)  $x \geq 0$

Question 11

Solve the polynomial equation by factoring.
-$$x ^ { 3 } - 16 x = 0$$

Accepted Answer

A)  $4 , - 4$ 
B)  $0,4 , - 4$ 
C)  $8 , - 8$ 
D)  $0,8 , - 8$ 
A)  $4 , - 4$ 
B)  $0,4 , - 4$ 
C)  $8 , - 8$ 
D)  $0,8 , - 8$

Question 12

Graph the function.
-$$f ( x ) = \frac { x - 4 } { x + 5 }$$

Accepted Answer

A)   
B)   
C)   
D)   
A)   
B)   
C)   
D)

Question 13

Suppose that during a flu epidemic in a particular city, the number of people, N(x), infected (in thousands) at the end of x
weeks is approximated by $N ( x ) = \frac { 104 x } { x + 28 }$ What is the horizontal asymptote of the graph of this function? What does this suggest about the maximum number of
people who will eventually be infected? Explain your reasoning.

Accepted Answer

The horizontal asymptote is @#LAT-DLM& . This sugg

Question 14

Solve the polynomial equation by factoring.
-$$x ^ { 3 } + 3 x ^ { 2 } - x - 3 = 0$$

Accepted Answer

A)  $1 , - 1,3$ 
B)  $1 , - 1 , - 4$ 
C)  $1 , - 2,5$ 
D)  $1 , - 1 , - 3$ 
A)  $1 , - 1,3$ 
B)  $1 , - 1 , - 4$ 
C)  $1 , - 2,5$ 
D)  $1 , - 1 , - 3$

Question 15

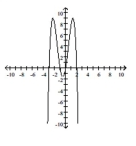
Use the given graph of the polynomial function to estimate the x-intercepts.
-

Accepted Answer

A)  $- 3 , - 1,2$ 
B)  $- 3 , - 1,2$. 
C)  $- 3 , - 1,0,2$ 
D)  $- 1,0,2$ 
A)  $- 3 , - 1,2$ 
B)  $- 3 , - 1,2$. 
C)  $- 3 , - 1,0,2$ 
D)  $- 1,0,2$

Question 16

Match the polynomial function with the graph.
-$$y = - 2 x ^ { 3 } - 4 x ^ { 2 } + 24 x + 15$$

Accepted Answer

A)   
B)   
C)   
D)   
A)   
B)   
C)   
D)

Question 17

Provide an appropriate response.
-If the average cost per unit C(x) to produce x units of plywood is given by $C ( x ) = \frac { 900 } { x + 30 }$ , what is the unit cost for 10 units? Round to the nearest cent.

Accepted Answer

A)  $60.00 
B)  $3.00 
C)  $22.50 
D)  $90.00 
A)  $60.00 
B)  $3.00 
C)  $22.50 
D)  $90.00

Question 18

The table below gives the violent crime rate (per 100,000 people) for a particular state every five years from 1970 to 2010. $$\begin{array} { c | c } 
\text { Year } & \begin{array} { c } 
\text { Violent Crime } \
\text { Rate }
\end{array} \
\hline 1970 & 4.8 \
\hline 1975 & 5.0 \
\hline 1980 & 5.9 \
\hline 1985 & 7.3 \
\hline 1990 & 8.9 \
\hline 1995 & 10.4 \
\hline 2000 & 11.6 \
\hline 2005 & 12.3 \
\hline 2010 & 12.1
\end{array}$$ Use technology to find the cubic function that is the best fit for this data, where x is the number of years after 1970. Use the model to estimate the year having a violent crime rate of 11.4 per 100,000.

Accepted Answer

A)  2012 
B)  2016 
C)  2011 
D)  2014 
A)  2012 
B)  2016 
C)  2011 
D)  2014

Question 19

For the given rational function, find all values of x for which y has the indicated value.
-$$y = \frac { 12 } { x } - \frac { 12 } { 3 x } ; \quad y = 6$$

Accepted Answer

A)  $\frac { 8 } { 3 }$ 
B)  $\frac { 17 } { 6 }$ 
C)  $\frac { 4 } { 3 }$ 
D)  $\frac { 5 } { 3 }$ 
A)  $\frac { 8 } { 3 }$ 
B)  $\frac { 17 } { 6 }$ 
C)  $\frac { 4 } { 3 }$ 
D)  $\frac { 5 } { 3 }$

Question 20

A retailer knows that n games can be sold in a month if the price is 30-0.2n  dollars per game. if he buys each game foe $18, and if he wishes to make a profit of at least $160 per month on sales of this game, how many games must he sell each month?

Accepted Answer

A)  20Games $\leq \mathbf { n } \leq$60 Games 
B) 20Games$\leq \mathbf { n } \leq$  40 Games 
C)  20 Games$\leq \mathbf { n } \leq$  20 Games 
D)  20 Games$\leq \mathbf { n } \leq$30 Games 
A)  20Games $\leq \mathbf { n } \leq$60 Games 
B) 20Games$\leq \mathbf { n } \leq$  40 Games 
C)  20 Games$\leq \mathbf { n } \leq$  20 Games 
D)  20 Games$\leq \mathbf { n } \leq$30 Games

Determine all possible rational solutions of the polynomial equation. - $f ( x ) = 6 x ^ { 3 } + 24 x ^ { 2 } + 2 x - 3$

State the degree and leading coefficient of the polynomial function. - $f ( x ) = - 8 + 10 x ^ { 4 } + 13 x - 3 x ^ { 3 } - 7 x ^ { 2 }$

Use analytical methods to solve the equation. - $\frac { x + 1 } { 2 } = \frac { x + 2 } { 3 }$

Determine whether the given constant is a solution to the given polynomial equation. - $- x ^ { 4 } + 5 x ^ { 2 } - x - 2 = 0 ; - 1$

Use the graph of f(x) to solve the inequality. - $f(x)>0$

Solve the polynomial equation by factoring. - $x ^ { 3 } - 16 x = 0$

Graph the function. - $f ( x ) = \frac { x - 4 } { x + 5 }$ $Graph the function. - f ( x ) = \frac { x - 4 } { x + 5 }$

Solve the polynomial equation by factoring. - $x ^ { 3 } + 3 x ^ { 2 } - x - 3 = 0$

Use the given graph of the polynomial function to estimate the x-intercepts. -

Match the polynomial function with the graph. - $y = - 2 x ^ { 3 } - 4 x ^ { 2 } + 24 x + 15$

Provide an appropriate response. -If the average cost per unit C(x) to produce x units of plywood is given by $C ( x ) = \frac { 900 } { x + 30 }$ , what is the unit cost for 10 units? Round to the nearest cent.

For the given rational function, find all values of x for which y has the indicated value. - $y = \frac { 12 } { x } - \frac { 12 } { 3 x } ; \quad y = 6$

A retailer knows that n games can be sold in a month if the price is 30-0.2n dollars per game. if he buys each game foe $18, and if he wishes to make a profit of at least $160 per month on sales of this game, how many games must he sell each month?

Functions, Graphs, and Models; Linear Functions

Linear Models, Equations, and Inequalities

Quadratic, Piecewise-Defined, and Power Functions

Additional Topics With Functions

Exponential and Logarithmic Functions

Systems of Equations and Matrices

Special Topics in Algebra

Filters

Exam 6: Higher-Degree Polynomial and Rational Functions

Determine all possible rational solutions of the polynomial equation. - f(x)=6x3+24x2+2x−3f ( x ) = 6 x ^ { 3 } + 24 x ^ { 2 } + 2 x - 3f(x)=6x3+24x2+2x−3

State the degree and leading coefficient of the polynomial function. - f(x)=−8+10x4+13x−3x3−7x2f ( x ) = - 8 + 10 x ^ { 4 } + 13 x - 3 x ^ { 3 } - 7 x ^ { 2 }f(x)=−8+10x4+13x−3x3−7x2

Use analytical methods to solve the equation. - x+12=x+23\frac { x + 1 } { 2 } = \frac { x + 2 } { 3 }2x+1​=3x+2​

Determine whether the given constant is a solution to the given polynomial equation. - −x4+5x2−x−2=0;−1- x ^ { 4 } + 5 x ^ { 2 } - x - 2 = 0 ; - 1−x4+5x2−x−2=0;−1

Use the graph of f(x) to solve the inequality. - f(x)>0f(x)>0f(x)>0

Solve the polynomial equation by factoring. - x3−16x=0x ^ { 3 } - 16 x = 0x3−16x=0

Graph the function. - f(x)=x−4x+5f ( x ) = \frac { x - 4 } { x + 5 }f(x)=x+5x−4​

Solve the polynomial equation by factoring. - x3+3x2−x−3=0x ^ { 3 } + 3 x ^ { 2 } - x - 3 = 0x3+3x2−x−3=0