Exam 6: Higher-Degree Polynomial and Rational Functions
Exam 1: Functions, Graphs, and Models; Linear Functions306 Questions
Exam 2: Linear Models, Equations, and Inequalities212 Questions
Exam 3: Quadratic, Piecewise-Defined, and Power Functions261 Questions
Exam 4: Additional Topics With Functions299 Questions
Exam 5: Exponential and Logarithmic Functions304 Questions
Exam 6: Higher-Degree Polynomial and Rational Functions262 Questions
Exam 7: Systems of Equations and Matrices196 Questions
Exam 8: Special Topics in Algebra265 Questions
Select questions type
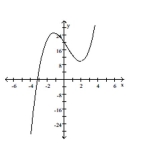
Determine whether the polynomial function is cubic or quartic.
-
(Multiple Choice)
4.9/5  (42)
(42)
Use synthetic division to find the quotient and remainder.
-
(Multiple Choice)
4.8/5  (33)
(33)
Use a graphing calculator to estimate the local maximum and local minimum values of the function to the nearest
hundredth.
-The polynomial measures the concentration of a dye in the bloodstream x seconds after it is injected. Does the concentration increase between 12 and 13 seconds?
(Multiple Choice)
4.7/5  (30)
(30)
Use algebraic and/or graphical methods to solve the inequality.
-
(Multiple Choice)
4.7/5  (39)
(39)
At a ticket booth, customers arrive randomly at a rate of x per hour. The average line length is where To keep the time waiting in line reasonable, it is decided that the average line length should not exceed 6 customers. Solve the inequality to determine the rates x per hour at which customers can arrive before a second attendant is needed.
(Multiple Choice)
4.9/5  (44)
(44)
Provide an appropriate response.
-If Q varies inversely as the square roo , what is Q when R is 16?
(Multiple Choice)
4.9/5  (32)
(32)
One solution of a polynomial equation is given. Use synthetic division to find any remaining solutions.
-
(Multiple Choice)
4.7/5  (34)
(34)
Use algebraic and/or graphical methods to solve the inequality.
-
(Multiple Choice)
4.8/5  (30)
(30)
Give the equations of any vertical asymptotes for the graphs of the rational functions.
-
(Multiple Choice)
4.9/5  (30)
(30)
The future value of $7000 invested for 5 years at rate r, compounded annually, is given by Find the rate r, as a percent, that gives a future value of $9817.86. Round to the nearest whole percent.
(Multiple Choice)
4.8/5  (33)
(33)
Determine all possible rational solutions of the polynomial equation.
-
(Multiple Choice)
4.7/5  (30)
(30)
An open-top box is to be made by cutting small identical squares from each corner of a 12 -by-12-in. sheet of tin and bending up the sides. If each corner square is x inches on a side, the volume of the box (in in. 3) is given by . By sketching the graph of V(x) , estimate what values of x result in a box with a volume greater than 64 in3 .
(Multiple Choice)
4.9/5  (30)
(30)
Suppose a cost-benefit model is given b where y is the cost in thousands of dollars for removing x percent of a given pollutant. Find the cost of removing 45% to the nearest dollar.
(Multiple Choice)
4.8/5  (28)
(28)
Use graphical methods to find any turning points of the graph of the function.
-
(Multiple Choice)
4.7/5  (37)
(37)
Showing 141 - 160 of 262
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)