Exam 6: Higher-Degree Polynomial and Rational Functions
Exam 1: Functions, Graphs, and Models; Linear Functions306 Questions
Exam 2: Linear Models, Equations, and Inequalities212 Questions
Exam 3: Quadratic, Piecewise-Defined, and Power Functions261 Questions
Exam 4: Additional Topics With Functions299 Questions
Exam 5: Exponential and Logarithmic Functions304 Questions
Exam 6: Higher-Degree Polynomial and Rational Functions262 Questions
Exam 7: Systems of Equations and Matrices196 Questions
Exam 8: Special Topics in Algebra265 Questions
Select questions type
For the given rational function, find all values of x for which y has the indicated value.
-
(Multiple Choice)
4.8/5  (30)
(30)
State the degree and leading coefficient of the polynomial function.
-
(Multiple Choice)
4.9/5  (39)
(39)
A new health food store runs an advertising campaign. Daily sales (in dollars) after x days of advertising are given by By sketching the graph of this function, answer the following questions. What is the horizontal asymptote of the graph?
What does this suggest about future sales? Explain your reasoning. If the advertising campaign costs $3200 per day, at
what point should it be discontinued? Why?
(Essay)
4.9/5  (30)
(30)
Ariel, a marine biologist, models a population P of crabs, t days after being left to reproduce, with the function . Assuming that this model continues to be accurate, when will this population become extinct? (Round to the nearest day.)
(Multiple Choice)
4.9/5  (33)
(33)
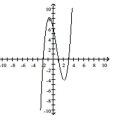
Use the given graph of the polynomial function to estimate the x-intercepts.
-
(Multiple Choice)
4.9/5  (37)
(37)
Use synthetic division to find the quotient and remainder.
-
(Multiple Choice)
4.9/5  (27)
(27)
Suppose that a cost-benefit model is given by where f(x) is the cost in thousands of dollars of removing x percent of a given pollutant. What is the vertical asymptote of the graph of this function? What does this suggest about the possibility of removing all of the pollutant? Explain your
reasoning.
(Essay)
4.9/5  (25)
(25)
Give the equations of any vertical asymptotes for the graphs of the rational functions.
-
(Multiple Choice)
4.9/5  (34)
(34)
Determine a window that will provide a comprehensive graph of the polynomial function.
-
(Multiple Choice)
4.8/5  (37)
(37)
Choose the graph that satisfies the given conditions.
-Polynomial of degree 4 with two distinc s and a negative leading coefficient
(Multiple Choice)
4.8/5  (37)
(37)
The price for a product is given by be sold to give positive revenue?
, where x is the number of units sold. How many units must
(Multiple Choice)
4.8/5  (31)
(31)
Find one solution graphically and then find the remaining solutions using synthetic division.
-3x4 + 2x3 - 76x2 - 50x + 25 = 0
(Multiple Choice)
4.9/5  (34)
(34)
Choose the graph that satisfies the given conditions.
-Degree 4 with four x s and a negative leading coefficient
(Multiple Choice)
4.8/5  (35)
(35)
Determine a window that will provide a comprehensive graph of the polynomial function.
-
(Multiple Choice)
4.8/5  (42)
(42)
State the degree and leading coefficient of the polynomial function.
-
(Multiple Choice)
4.8/5  (37)
(37)
Showing 61 - 80 of 262
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)