Question 1

Find the cubic or quartic function that models the data in the table.
-$\begin{array}{r|rrrrr}
x & 0 & 3 & 7 & 9 & 11 \
\hline y & -1 & 5 & 9 & 15 & 19
\end{array} \text { (Quartic }$

Accepted Answer

A)  $y = - 0.02 x ^ { 4 } + 0.22 x ^ { 3 } + 1.96 x ^ { 2 } - 5.72 x - 1.00$ 
B)  $y = - 0.01 x ^ { 4 } - 0.27 x ^ { 3 } + 1.94 x ^ { 2 } + 5.70 x - 1.00$ 
C)  $y = 0.01 x ^ { 4 } + 0.22 x ^ { 3 } - 1.94 x ^ { 2 } - 5.72 x - 1.00$ 
D)  $y = - 0.01 x ^ { 4 } + 0.27 x ^ { 3 } - 1.94 x ^ { 2 } + 5.70 x - 1.00$ 
A)  $y = - 0.02 x ^ { 4 } + 0.22 x ^ { 3 } + 1.96 x ^ { 2 } - 5.72 x - 1.00$ 
B)  $y = - 0.01 x ^ { 4 } - 0.27 x ^ { 3 } + 1.94 x ^ { 2 } + 5.70 x - 1.00$ 
C)  $y = 0.01 x ^ { 4 } + 0.22 x ^ { 3 } - 1.94 x ^ { 2 } - 5.72 x - 1.00$ 
D)  $y = - 0.01 x ^ { 4 } + 0.27 x ^ { 3 } - 1.94 x ^ { 2 } + 5.70 x - 1.00$

Question 2

Solve the equation exactly in the complex number system.
-$$x ^ { 3 } + 125 = 0$$

Accepted Answer

A)  $x = - \frac { 5 } { 2 } , x = \frac { 5 } { 2 } \pm \frac { 5 i \sqrt { 3 } } { 2 }$ 
B)  $x = - 5 , x = \frac { 5 } { 2 } + \frac { 5 i \sqrt { 3 } } { 2 } , x = - \frac { 5 } { 2 } - \frac { 5 i \sqrt { 3 } } { 2 }$ 
C)  $x = 5 , x = \frac { 5 } { 2 } \pm \frac { 5 i \sqrt { 3 } } { 2 }$ 
D)  $x = - 5 , x = \frac { 5 } { 2 } \pm \frac { 5 i \sqrt { 3 } } { 2 }$ 
A)  $x = - \frac { 5 } { 2 } , x = \frac { 5 } { 2 } \pm \frac { 5 i \sqrt { 3 } } { 2 }$ 
B)  $x = - 5 , x = \frac { 5 } { 2 } + \frac { 5 i \sqrt { 3 } } { 2 } , x = - \frac { 5 } { 2 } - \frac { 5 i \sqrt { 3 } } { 2 }$ 
C)  $x = 5 , x = \frac { 5 } { 2 } \pm \frac { 5 i \sqrt { 3 } } { 2 }$ 
D)  $x = - 5 , x = \frac { 5 } { 2 } \pm \frac { 5 i \sqrt { 3 } } { 2 }$

Question 3

Graph the function.
-$$f ( x ) = \frac { 4 x + 1 } { x + 2 }$$

Accepted Answer

A)   
B)   
C)   
D)   
A)   
B)   
C)   
D)

Question 4

Use factoring by grouping to solve the equation.
-$$5 x ^ { 3 } + 3 x ^ { 2 } - 125 x - 75 = 0$$

Accepted Answer

A)  $- 5,5 , \frac { 3 } { 5 }$ 
B)  $- \frac { 5 } { 3 } , - 5,1$ 
C)  $- \frac { 3 } { 5 } , - 5,5$ 
D)  $- \frac { 5 } { 3 } , - 5,5$ 
A)  $- 5,5 , \frac { 3 } { 5 }$ 
B)  $- \frac { 5 } { 3 } , - 5,1$ 
C)  $- \frac { 3 } { 5 } , - 5,5$ 
D)  $- \frac { 5 } { 3 } , - 5,5$

Question 5

Predict the end behavior of the graph of the function.
-$$f ( x ) = - x ^ { 3 } - 9 x ^ { 2 } - 3 x + 3$$

Accepted Answer

A)  Down on both sides 
B)  Up on left side, down on right side 
C)  Down on left side, up on right side 
D)  Up on both sides 
A)  Down on both sides 
B)  Up on left side, down on right side 
C)  Down on left side, up on right side 
D)  Up on both sides

Question 6

$x ^ { 3 } + 10 x ^ { 2 } + 31 x \leq - 30$

Accepted Answer

A)  $- 5 \leq x \leq - 3 \text { or } x \geq - 2$ 
B)  $x < - 5 \text { or } - 3 < x < - 2$ 
C)  $x \leq 2 \text { or } 3 \leq x \leq 5$ 
D)  $x \leq - 5 \text { or } - 3 \leq x \leq - 2$ 
A)  $- 5 \leq x \leq - 3 \text { or } x \geq - 2$ 
B)  $x < - 5 \text { or } - 3 < x < - 2$ 
C)  $x \leq 2 \text { or } 3 \leq x \leq 5$ 
D)  $x \leq - 5 \text { or } - 3 \leq x \leq - 2$

Question 7

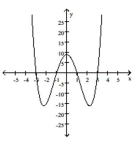
Use the graph of the polynomial function f(x) to solve f( $$f ( x ) \text { to solve } f ( x ) = 0$$
-

Accepted Answer

A)  $- 4 , - 1,1,4$ 
B)  $- 3 , - 1$ 
C)  $- 3 , - 1,1,3$ 
D)  1,3 
A)  $- 4 , - 1,1,4$ 
B)  $- 3 , - 1$ 
C)  $- 3 , - 1,1,3$ 
D)  1,3

Question 8

$f ( x ) = 3 x ^ { 3 } - 26 x ^ { 2 } + 18 x - 47$

Accepted Answer

A)   [-5,5]  by  [-500,100] 
B)   [-8,10]  by  [-100,300] 
C)   [-3,10]  by  [-400,100] 
D)   [-10,10]  by  [-150,150] 
A)   [-5,5]  by  [-500,100] 
B)   [-8,10]  by  [-100,300] 
C)   [-3,10]  by  [-400,100] 
D)   [-10,10]  by  [-150,150]

Question 9

The table below gives the violent crime rate (per 100,000 people) for a particular state every five years from 1970 to 2010. $\begin{array} { c | c } 
\text { Year } & \begin{array} { c } 
\text { Violent Crime } \
\text { Rate }
\end{array} \
\hline 1970 & 4.8 \
\hline 1975 & 5.0 \
\hline 1980 & 5.9 \
\hline 1985 & 7.3 \
\hline 1990 & 8.9 \
\hline 1995 & 10.4 \
\hline 2000 & 11.6 \
\hline 2005 & 12.3 \
\hline 2010 & 12.1
\end{array}$ 
Use technology to find the cubic function that is the best fit for this data, where x is the number of years after 1970. Round to five decimal places.

Accepted Answer

A)  $y = - 0.00034 x ^ { 3 } + 0.01950 x ^ { 2 } - 0.04893 x + 4.79798$ 
B)  $y = 4.79798 x ^ { 3 } - 0.04893 x ^ { 2 } + 0.01950 x - 0.00034$ 
C)  $y = - 0.00024 x ^ { 3 } + 0.02250 x ^ { 2 } - 0.03111 x + 4.68687$ 
D)  $y = - 0.00053 x ^ { 3 } + 0.02460 x ^ { 2 } - 0.01893 x + 5.79798$ 
A)  $y = - 0.00034 x ^ { 3 } + 0.01950 x ^ { 2 } - 0.04893 x + 4.79798$ 
B)  $y = 4.79798 x ^ { 3 } - 0.04893 x ^ { 2 } + 0.01950 x - 0.00034$ 
C)  $y = - 0.00024 x ^ { 3 } + 0.02250 x ^ { 2 } - 0.03111 x + 4.68687$ 
D)  $y = - 0.00053 x ^ { 3 } + 0.02460 x ^ { 2 } - 0.01893 x + 5.79798$

Question 10

A rectangular piece of cardboard measuring 15 inches by 29 inches is to be made into a box with an open top by cutting equal size squares from each corner and folding up the sides. Let x represent the length of a side of each
Such square. For what value of x will the volume be a maximum? If necessary, round to 2 decimal places.

Accepted Answer

A)  13.79 in. 
B)  3.15 in. 
C)  11.52 in. 
D)  23.04 in. 
A)  13.79 in. 
B)  3.15 in. 
C)  11.52 in. 
D)  23.04 in.

Question 11

One solution of a polynomial equation is given. Use synthetic division to find any remaining solutions.
-$- 2 x ^ { 3 } - 4 x ^ { 2 } + 2 x + 4 = 0 ; 1$

Accepted Answer

A)  1,2 
B)  $- 1 , - 2$ 
C)  $1 , - 2$ 
D)  $- 1,2$ 
A)  1,2 
B)  $- 1 , - 2$ 
C)  $1 , - 2$ 
D)  $- 1,2$

Question 12

Use graphical methods to find any turning points of the graph of the function.
-$$y = \frac { x + 1 } { x ^ { 2 } + 3 x + 3 }$$

Accepted Answer

A)  No turning points 
B)  $\left( 0 , \frac { 1 } { 3 } \right)$ and $( - 2 , - 1 )$ 
C)  $( 0,3 )$ and $\left( - 2 , \frac { 1 } { 3 } \right)$ 
D)  $\left( 0 , - \frac { 1 } { 3 } \right)$ and $( - 2,1 )$ 
A)  No turning points 
B)  $\left( 0 , \frac { 1 } { 3 } \right)$ and $( - 2 , - 1 )$ 
C)  $( 0,3 )$ and $\left( - 2 , \frac { 1 } { 3 } \right)$ 
D)  $\left( 0 , - \frac { 1 } { 3 } \right)$ and $( - 2,1 )$

Question 13

The average number of vehicles waiting in line at a toll booth of a super highway is modeled by the function $\mathrm { n } ( \mathrm { x } ) = \frac { \mathrm { x } ^ { 2 } } { 0.5 ( 1 - \mathrm { x } ) }$ , where x is a quantity between 0 and 1 known as the traffic intensity. To the nearest tenth, find the average number of vehicles waiting if the traffic intensity is .81.

Accepted Answer

A)  1.6 vehicles 
B)  3.5 vehicles 
C)  6.9 vehicles 
D)  8.5 vehicles 
A)  1.6 vehicles 
B)  3.5 vehicles 
C)  6.9 vehicles 
D)  8.5 vehicles

Question 14

Determine all possible rational solutions of the polynomial equation.
-$$f ( x ) = 2 x ^ { 3 } + 8 x ^ { 2 } + 12 x - 8$$

Accepted Answer

A)  $\pm 1 , \pm 2 , \pm 4 , \pm 8$ 
B)  $\pm 1 , \pm \frac { 1 } { 2 } , \pm 2 , \pm 4 , \pm 8$ 
C)  $\pm 1 , \pm 2 , \pm 4$ 
D)  $\pm 1 , \pm \frac { 1 } { 2 } , \pm \frac { 1 } { 4 } , \pm \frac { 1 } { 8 } , \pm 2$ 
A)  $\pm 1 , \pm 2 , \pm 4 , \pm 8$ 
B)  $\pm 1 , \pm \frac { 1 } { 2 } , \pm 2 , \pm 4 , \pm 8$ 
C)  $\pm 1 , \pm 2 , \pm 4$ 
D)  $\pm 1 , \pm \frac { 1 } { 2 } , \pm \frac { 1 } { 4 } , \pm \frac { 1 } { 8 } , \pm 2$

Question 15

Match the polynomial function with the graph.
-$$y = 3 x ^ { 3 } + 3 x ^ { 2 } - 21 x - 15$$

Accepted Answer

A)   
B)   
C)   
D)   
A)   
B)   
C)   
D)

Question 16

Determine all possible rational solutions of the polynomial equation.
-$$f ( x ) = 2 x ^ { 3 } - 5 x ^ { 2 } + 7 x - 17$$

Accepted Answer

A)  $\pm 1 , \pm 2 , \pm 17 , \pm \frac { 17 } { 2 }$ 
B)  $\pm 1 , \pm 2 , \pm 17$ 
C)  $\pm 1 , \pm 17 , \pm \frac { 1 } { 2 } , \pm \frac { 17 } { 2 }$ 
D)  $\pm 1 , \pm \frac { 1 } { 17 } , \pm 2 , \pm \frac { 2 } { 17 }$ 
A)  $\pm 1 , \pm 2 , \pm 17 , \pm \frac { 17 } { 2 }$ 
B)  $\pm 1 , \pm 2 , \pm 17$ 
C)  $\pm 1 , \pm 17 , \pm \frac { 1 } { 2 } , \pm \frac { 17 } { 2 }$ 
D)  $\pm 1 , \pm \frac { 1 } { 17 } , \pm 2 , \pm \frac { 2 } { 17 }$

Question 17

The average waiting time in a line before getting served is given by
W = S(S A-A)
where A is the average rate that people arrive at the line and S is the average service time. At a certain bank, the average service time is 4 minutes. By sketching a graph of the equation on the interval (0, 4], answer the following questions.
What happens to W when A is close to zero? Why does this make sense? What feature of your graph gives this information?

Accepted Answer

As A approaches zero, the waiting time,

Question 18

$4 x ^ { 3 } + 5 x ^ { 2 } - 23 x - 6 = 0 ; - 3$

Accepted Answer

A)   2,-$\frac { 1 } { 4 }$ 
B)   2,-1 
C)   -2 ,$\frac { 1 } { 4 }$ 
D)   3,-2,1 
A)   2,-$\frac { 1 } { 4 }$ 
B)   2,-1 
C)   -2 ,$\frac { 1 } { 4 }$ 
D)   3,-2,1

Question 19

Use factoring by grouping to solve the equation.
-$$2 x ^ { 3 } + 8 x ^ { 2 } - 8 x - 32 = 0$$

Accepted Answer

A)  $- 4 , - 2,1$ 
B)  $- 4 , - 2,2$ 
C)  $- 8 , - 4,4$ 
D)  $- 2,2,4$ 
A)  $- 4 , - 2,1$ 
B)  $- 4 , - 2,2$ 
C)  $- 8 , - 4,4$ 
D)  $- 2,2,4$

Question 20

Solve the polynomial equation by using the root method.
-$$\frac { 1 } { 5 } x ^ { 4 } - 125 = 0$$

Accepted Answer

A)  $5 , - 5$ 
B)  $- 5$ 
C)  5 
D)  5,0 
A)  $5 , - 5$ 
B)  $- 5$ 
C)  5 
D)  5,0

Find the cubic or quartic function that models the data in the table. - x 0 3 7 9 11 y -1 5 9 15 19 start text left parenthesisQuartic end text

Solve the equation exactly in the complex number system. - $x ^ { 3 } + 125 = 0$

Graph the function. - $f ( x ) = \frac { 4 x + 1 } { x + 2 }$ $Graph the function. - f ( x ) = \frac { 4 x + 1 } { x + 2 }$

Use factoring by grouping to solve the equation. - $5 x ^ { 3 } + 3 x ^ { 2 } - 125 x - 75 = 0$

Predict the end behavior of the graph of the function. - $f ( x ) = - x ^ { 3 } - 9 x ^ { 2 } - 3 x + 3$

$x ^ { 3 } + 10 x ^ { 2 } + 31 x \leq - 30$

Use the graph of the polynomial function f(x) to solve f( $f ( x ) \text { to solve } f ( x ) = 0$ - $Use the graph of the polynomial function f(x) to solve f( f ( x ) \text { to solve } f ( x ) = 0 -$

$f ( x ) = 3 x ^ { 3 } - 26 x ^ { 2 } + 18 x - 47$

One solution of a polynomial equation is given. Use synthetic division to find any remaining solutions. - $- 2 x ^ { 3 } - 4 x ^ { 2 } + 2 x + 4 = 0 ; 1$

Use graphical methods to find any turning points of the graph of the function. - $y = \frac { x + 1 } { x ^ { 2 } + 3 x + 3 }$

Determine all possible rational solutions of the polynomial equation. - $f ( x ) = 2 x ^ { 3 } + 8 x ^ { 2 } + 12 x - 8$

Match the polynomial function with the graph. - $y = 3 x ^ { 3 } + 3 x ^ { 2 } - 21 x - 15$

Determine all possible rational solutions of the polynomial equation. - $f ( x ) = 2 x ^ { 3 } - 5 x ^ { 2 } + 7 x - 17$

$4 x ^ { 3 } + 5 x ^ { 2 } - 23 x - 6 = 0 ; - 3$

Use factoring by grouping to solve the equation. - $2 x ^ { 3 } + 8 x ^ { 2 } - 8 x - 32 = 0$

Solve the polynomial equation by using the root method. - $\frac { 1 } { 5 } x ^ { 4 } - 125 = 0$

Functions, Graphs, and Models; Linear Functions

Linear Models, Equations, and Inequalities

Quadratic, Piecewise-Defined, and Power Functions

Additional Topics With Functions

Exponential and Logarithmic Functions

Systems of Equations and Matrices

Special Topics in Algebra

Filters

Exam 6: Higher-Degree Polynomial and Rational Functions

Find the cubic or quartic function that models the data in the table. - x 0 3 7 9 11 y -1 5 9 15 19 start text left parenthesisQuartic end text

Solve the equation exactly in the complex number system. - x3+125=0x ^ { 3 } + 125 = 0x3+125=0

Graph the function. - f(x)=4x+1x+2f ( x ) = \frac { 4 x + 1 } { x + 2 }f(x)=x+24x+1​

Use factoring by grouping to solve the equation. - 5x3+3x2−125x−75=05 x ^ { 3 } + 3 x ^ { 2 } - 125 x - 75 = 05x3+3x2−125x−75=0

Predict the end behavior of the graph of the function. - f(x)=−x3−9x2−3x+3f ( x ) = - x ^ { 3 } - 9 x ^ { 2 } - 3 x + 3f(x)=−x3−9x2−3x+3

x3+10x2+31x≤−30x ^ { 3 } + 10 x ^ { 2 } + 31 x \leq - 30x3+10x2+31x≤−30

Use the graph of the polynomial function f(x) to solve f( f(x) to solve f(x)=0f ( x ) \text { to solve } f ( x ) = 0f(x) to solve f(x)=0 -

f(x)=3x3−26x2+18x−47f ( x ) = 3 x ^ { 3 } - 26 x ^ { 2 } + 18 x - 47f(x)=3x3−26x2+18x−47

One solution of a polynomial equation is given. Use synthetic division to find any remaining solutions. - −2x3−4x2+2x+4=0;1- 2 x ^ { 3 } - 4 x ^ { 2 } + 2 x + 4 = 0 ; 1−2x3−4x2+2x+4=0;1

Use graphical methods to find any turning points of the graph of the function. - y=x+1x2+3x+3y = \frac { x + 1 } { x ^ { 2 } + 3 x + 3 }y=x2+3x+3x+1​

Determine all possible rational solutions of the polynomial equation. - f(x)=2x3+8x2+12x−8f ( x ) = 2 x ^ { 3 } + 8 x ^ { 2 } + 12 x - 8f(x)=2x3+8x2+12x−8

Match the polynomial function with the graph. - y=3x3+3x2−21x−15y = 3 x ^ { 3 } + 3 x ^ { 2 } - 21 x - 15y=3x3+3x2−21x−15

Determine all possible rational solutions of the polynomial equation. - f(x)=2x3−5x2+7x−17f ( x ) = 2 x ^ { 3 } - 5 x ^ { 2 } + 7 x - 17f(x)=2x3−5x2+7x−17

4x3+5x2−23x−6=0;−34 x ^ { 3 } + 5 x ^ { 2 } - 23 x - 6 = 0 ; - 34x3+5x2−23x−6=0;−3

Use factoring by grouping to solve the equation. - 2x3+8x2−8x−32=02 x ^ { 3 } + 8 x ^ { 2 } - 8 x - 32 = 02x3+8x2−8x−32=0

Solve the polynomial equation by using the root method. - 15x4−125=0\frac { 1 } { 5 } x ^ { 4 } - 125 = 051​x4−125=0

Functions, Graphs, and Models; Linear Functions

Linear Models, Equations, and Inequalities

Quadratic, Piecewise-Defined, and Power Functions

Additional Topics With Functions

Exponential and Logarithmic Functions

Systems of Equations and Matrices

Special Topics in Algebra

Filters

Solve the equation exactly in the complex number system. - $x ^ { 3 } + 125 = 0$

Graph the function. - $f ( x ) = \frac { 4 x + 1 } { x + 2 }$ $Graph the function. - f ( x ) = \frac { 4 x + 1 } { x + 2 }$

Use factoring by grouping to solve the equation. - $5 x ^ { 3 } + 3 x ^ { 2 } - 125 x - 75 = 0$

Predict the end behavior of the graph of the function. - $f ( x ) = - x ^ { 3 } - 9 x ^ { 2 } - 3 x + 3$

$x ^ { 3 } + 10 x ^ { 2 } + 31 x \leq - 30$

Use the graph of the polynomial function f(x) to solve f( $f ( x ) \text { to solve } f ( x ) = 0$ - $Use the graph of the polynomial function f(x) to solve f( f ( x ) \text { to solve } f ( x ) = 0 -$

$f ( x ) = 3 x ^ { 3 } - 26 x ^ { 2 } + 18 x - 47$

One solution of a polynomial equation is given. Use synthetic division to find any remaining solutions. - $- 2 x ^ { 3 } - 4 x ^ { 2 } + 2 x + 4 = 0 ; 1$

Use graphical methods to find any turning points of the graph of the function. - $y = \frac { x + 1 } { x ^ { 2 } + 3 x + 3 }$

Determine all possible rational solutions of the polynomial equation. - $f ( x ) = 2 x ^ { 3 } + 8 x ^ { 2 } + 12 x - 8$

Match the polynomial function with the graph. - $y = 3 x ^ { 3 } + 3 x ^ { 2 } - 21 x - 15$

Determine all possible rational solutions of the polynomial equation. - $f ( x ) = 2 x ^ { 3 } - 5 x ^ { 2 } + 7 x - 17$

$4 x ^ { 3 } + 5 x ^ { 2 } - 23 x - 6 = 0 ; - 3$

Use factoring by grouping to solve the equation. - $2 x ^ { 3 } + 8 x ^ { 2 } - 8 x - 32 = 0$

Solve the polynomial equation by using the root method. - $\frac { 1 } { 5 } x ^ { 4 } - 125 = 0$