Exam 12: Further Topics in Algebra
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Solve the problem.
-What are the odds in favor of drawing a 3 from these cards?

(Multiple Choice)
4.7/5  (40)
(40)
Solve the problem.
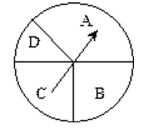
-What are the odds in favor of spinning a D on this spinner?
(Multiple Choice)
4.8/5  (41)
(41)
Find the probability.
-A lottery game contains 22 balls numbered 1 through 22 . What is the probability of choosing a ball numbered 23?
(Multiple Choice)
4.8/5  (35)
(35)
Find all natural number values for n for which the given statement is false.
-
(Multiple Choice)
5.0/5  (36)
(36)
Use mathematical induction to prove that the statement is true for every positive integer n.
-
(Essay)
5.0/5  (47)
(47)
Find the common ratio r for the given infinite geometric sequence.
-A small start-up consulting company hopes to have 7 times the clientele it had the previous year for the next 2 years. If the company just meets its targets each of the 2 years and it had 7 clients to
Begin with, how many clients does it have at the end of 2 years?
(Multiple Choice)
4.7/5  (44)
(44)
Use the sequence feature of a graphing calculator to evaluate the sum of the first 10 terms of the arithmetic sequence.
Round to the nearest thousandth, if necessary.
-The beginning population of a town was 36,000. If the population decreased by 250 people per year, how many people lived in the town 15 years later?
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-What are the odds in favor of spinning an A on this spinner? 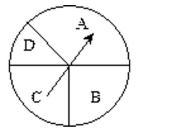
(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem.
-How many 4-digit numbers can be formed using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, if repetitions of digits are allowed?
(Multiple Choice)
4.8/5  (28)
(28)
Use a graphing calculator to evaluate the sum. Round to the nearest thousandth.
-
(Multiple Choice)
4.8/5  (50)
(50)
Write the first n terms of the given arithmetic sequence (the value of n is indicated in the question).
-
(Multiple Choice)
4.8/5  (33)
(33)
Use mathematical induction to prove that the statement is true for every positive integer n.
-The series of sketches below starts with an equilateral triangle having sides of length 1
(one). In the following steps, equilateral triangles are constructed by joining the midpoints
of the sides of the preceding triangle. Develop a formula for the area of the nth new
triangle. Use math induction to prove your answer. 
(Short Answer)
4.7/5  (32)
(32)
Evaluate the sum. Round to two decimal places, if necessary.
-
(Multiple Choice)
4.9/5  (46)
(46)
Use the summation properties to evaluate the series. The following rules may be needed:
-
(Multiple Choice)
4.7/5  (38)
(38)
Showing 181 - 200 of 348
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)