Exam 12: Further Topics in Algebra
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Solve the problem.
-An ordinary die is tossed. What are the odds in favor of the die showing a 4 ?
(Multiple Choice)
4.8/5  (41)
(41)
Write the first n terms of the given arithmetic sequence (the value of n is indicated in the question).
-
(Multiple Choice)
4.8/5  (34)
(34)
Write the indicated term of the binomial expansion.
- th term
(Multiple Choice)
4.9/5  (40)
(40)
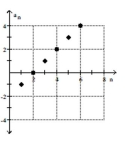
Find a formula for the nth term of the arithmetic sequence shown in the graph.
-
(Multiple Choice)
4.8/5  (31)
(31)
Graph the function corresponding to the sequence defined. Use the graph to decide whether the sequence converges or
diverges.
-Suppose that certain bacteria can double their size and divide every 30 minutes. Write a recursive sequence that describes this growth where each value of represents a 30 -minute interval. Let a 1 represent the initial number of bacteria present.
(Multiple Choice)
4.7/5  (42)
(42)
Use mathematical induction to prove that the statement is true for every positive integer n.
-
(Essay)
5.0/5  (39)
(39)
List the elements in the sample space of the experiment.
-A group of 13 people are assigned numbers 1 through 13 . List the sample space of the event choosing a person with a number 5 or less.
(Multiple Choice)
4.9/5  (46)
(46)
List the elements in the sample space of the experiment.
-A box contains 3 blue cards numbered 1 through 3 , and 4 green cards numbered 1 through 4 . List the sample space of picking a blue card followed by a green card.
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-A card is drawn from a well-shuffled deck of 52 cards. What is the probability of drawing an ace or 9?
(Multiple Choice)
4.7/5  (35)
(35)
Solve the problem.
-What are the odds in favor of drawing an even number from these cards?
 142454
142454
(Multiple Choice)
4.7/5  (38)
(38)
Solve the problem.
-A bag contains 6 apples and 4 oranges. If you select 5 pieces of fruit without looking, how many ways can you get 5 oranges?
(Multiple Choice)
4.8/5  (41)
(41)
Use mathematical induction to prove that the statement is true for every positive integer n.
-
(Essay)
4.7/5  (29)
(29)
Write the first n terms of the given arithmetic sequence (the value of n is indicated in the question).
-
(Multiple Choice)
4.9/5  (27)
(27)
Use mathematical induction to prove that the statement is true for every positive integer n.
-If , then .
(Assume that a is a constant.)
(Essay)
4.9/5  (44)
(44)
Solve the problem.
-Suppose there are 3 roads connecting town A to town B and 7 roads connecting town B to town C. In how many ways can a person travel from A to C via B?
(Multiple Choice)
4.8/5  (40)
(40)
Showing 81 - 100 of 348
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)