Exam 12: Further Topics in Algebra
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Solve the problem.
-How many different three-digit numbers can be written using digits from the set { without any repeating digits?
(Multiple Choice)
4.9/5  (30)
(30)
Write the indicated term of the binomial expansion.
- 3rd term
(Multiple Choice)
4.9/5  (38)
(38)
Decide whether the given sequence is finite or infinite.
--5, -4, -3, -2
(Multiple Choice)
4.8/5  (49)
(49)
Solve the problem.
-How many different three-number "combinations" are possible on a combination lock having 32 numbers on its dial without repeating a number?
(Multiple Choice)
4.9/5  (43)
(43)
Find all natural number values for n for which the given statement is false.
-
(Multiple Choice)
4.8/5  (42)
(42)
Write the first n terms of the given arithmetic sequence (the value of n is indicated in the question).
-3, 9, 15, 21, 27, . . .
(Multiple Choice)
4.8/5  (38)
(38)
Provide an appropriate response.
-Consider the arrangements of sixteen students in a line. Is this a combination, a permutation, or neither?
(Multiple Choice)
4.7/5  (34)
(34)
Solve the problem.
-A bag contains 5 apples and 3 oranges. If you select 4 pieces of fruit without looking, how many ways can you get exactly 3 apples?
(Multiple Choice)
4.9/5  (41)
(41)
Use mathematical induction to prove that the statement is true for every positive integer n.
-
(Essay)
4.9/5  (36)
(36)
It can be shown that . . . is true for any real number n (not just positive
integer values) and any real number x, wher . Use this series to approximate the given number to the nearest
thousandth.
-
(Multiple Choice)
4.9/5  (35)
(35)
Write the first n terms of the given arithmetic sequence (the value of n is indicated in the question).
-The first term is , and the common difference is
(Multiple Choice)
4.8/5  (38)
(38)
Find the common ratio r for the given infinite geometric sequence.
-A man borrowed $3000 at 1.5% interest compounded annually. If he paid off the loan in full at the end of 6 years, how much did he pay?
(Multiple Choice)
4.8/5  (37)
(37)
Find a formula for the nth term of the arithmetic sequence shown in the graph.
-
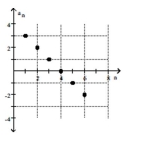
(Multiple Choice)
5.0/5  (44)
(44)
Showing 61 - 80 of 348
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)