Exam 16: Time-Series Forecasting

SCENARIO 16-15-B You are the CEO of a diary company. The total milk production (in gallons) from your company over the past 30 years are presented below and also contained in the Excel file SCENARIO 16- 15-B.XLSX. Year 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 Milk 150201 193718 212520 214553 237507 248069 241824 234627 252049 252029 Prod 263449 260689 247900 260059 268197 249477 246216 265236 256364 241705 245932 243529 241551 247697 248454 241974 235823 243517 238490 248606 You want to predict your company's future total milk production using the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model. -Referring to Scenario 16-15-B, you can reject the null hypothesis for testing the appropriateness of the second-order autoregressive model at the 5% level of significance.

SCENARIO 16-15-B You are the CEO of a diary company. The total milk production (in gallons) from your company over the past 30 years are presented below and also contained in the Excel file SCENARIO 16- 15-B.XLSX. Year 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 Milk 150201 193718 212520 214553 237507 248069 241824 234627 252049 252029 Prod 263449 260689 247900 260059 268197 249477 246216 265236 256364 241705 245932 243529 241551 247697 248454 241974 235823 243517 238490 248606 You want to predict your company's future total milk production using the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model. -Referring to Scenario 16-15-B, what is the exponentially smoothed value for 1997 using a smoothing coefficient of W = 0.5?

Which of the following terms describes the up and down movements of a time series that vary both in length and intensity?

SCENARIO 16-13 Given below is the monthly time series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the 1st month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 $\text { Quadratic trend model: }$ $\text { Exponential trend model: }$ Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 -Referring to Scenario 16-13, what is the value of the t test statistic for testing the appropriateness of the third-order autoregressive model?

When a time series appears to be increasing at an increasing rate, such that percentage difference from value to value is constant, the appropriate model to fit is the

SCENARIO 16-5 The number of passengers arriving at San Francisco on the Amtrak cross-country express on 6 successive Mondays were: 60, 72, 96, 84, 36, and 48. -Referring to Scenario 16-5, the number of arrivals will be smoothed with a 3-term moving average. The last smoothed value will be __________.

SCENARIO 16-15-A You are the CEO of a diary company. The total milk production (in gallons) from your company over the past 30 years are presented below and also contained in the Excel file SCENARIO 16- 15-A.XLSX. Year 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 Milk 150201 172719 171357 157121 155727 152974 153443 158548 162614 164210 Prod 159127 153866 165992 177843 167477 163821 161700 170348 174105 185103 184670 173385 159695 173641 165706 171164 168706 150684 179314 163802 You want to predict your company's future total milk production using the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model. -Referring to Scenario 16-15-A, you can conclude that the quadratic term in the quadratic-trend model is statistically significant at the 5% level of significance.

SCENARIO 16-5 The number of passengers arriving at San Francisco on the Amtrak cross-country express on 6 successive Mondays were: 60, 72, 96, 84, 36, and 48. -Referring to Scenario 16-5, the number of arrivals will be exponentially smoothed with a smoothing constant of 0.25. The forecast of the number of arrivals on the seventh Monday will be __________.

SCENARIO 16-15-A You are the CEO of a diary company. The total milk production (in gallons) from your company over the past 30 years are presented below and also contained in the Excel file SCENARIO 16- 15-A.XLSX. Year 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 Milk 150201 172719 171357 157121 155727 152974 153443 158548 162614 164210 Prod 159127 153866 165992 177843 167477 163821 161700 170348 174105 185103 184670 173385 159695 173641 165706 171164 168706 150684 179314 163802 You want to predict your company's future total milk production using the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model. -Referring to Scenario 16-15-A, you can reject the null hypothesis for testing the appropriateness of the first-order autoregressive model at the 5% level of significance.

SCENARIO 16-9 Given below are EXCEL outputs for various estimated autoregressive models for a company's real operating revenues (in billions of dollars) from 1989 to 2012. From the data, you also know that the real operating revenues for 2010, 2011, and 2012 are 11.7909, 11.7757 and 11.5537, respectively. First-Order Autoregressive Model: Coefficients Standard Eiror t Stat P -value Intercept 0.1802 0.3980 0.4528 0.6553 XLag1 1.0112 0.0497 20.3526 0.0000 Second-Order Autoregressive Model: Coefficients Standard Error t Stat P -value Intercept 0.3005 0.4408 0.6817 0.5036 X Lag 1 1.1732 0.2347 4.9980 0.0001 X Lag 2 -0.1830 0.2507 -0.7300 0.4743 Third-Order Autoregressive Model: Coefficients Standard Error t Stat P-value Intercept 0.3130 0.5144 0.6085 0.5509 XLag1 1.1737 0.2465 4.7617 0.0002 XLag2 -0.0694 0.3731 -0.1860 0.8547 XLag3 -0.1221 0.2820 -0.4330 0.6704 -Referring to Scenario 16-9, if one decides to use the Third-Order Autoregressive model , what will the predicted real operating revenue for the company be in 2013?

SCENARIO 16-11 The manager of a health club has recorded mean attendance in newly introduced step classes over the last 15 months: 32.1, 39.5, 40.3, 46.0, 65.2, 73.1, 83.7, 106.8, 118.0, 133.1, 163.3, 182.8, 205.6, 249.1, and 263.5. She then used Microsoft Excel to obtain the following partial output for both a first- and second-order autoregressive model. -Referring to Scenario 16-11, based on the parsimony principle, the second- order model is the better model for making forecasts.

SCENARIO 16-9 Given below are EXCEL outputs for various estimated autoregressive models for a company's real operating revenues (in billions of dollars) from 1989 to 2012. From the data, you also know that the real operating revenues for 2010, 2011, and 2012 are 11.7909, 11.7757 and 11.5537, respectively. First-Order Autoregressive Model: Coefficients Standard Eiror t Stat P -value Intercept 0.1802 0.3980 0.4528 0.6553 XLag1 1.0112 0.0497 20.3526 0.0000 Second-Order Autoregressive Model: Coefficients Standard Error t Stat P -value Intercept 0.3005 0.4408 0.6817 0.5036 X Lag 1 1.1732 0.2347 4.9980 0.0001 X Lag 2 -0.1830 0.2507 -0.7300 0.4743 Third-Order Autoregressive Model: Coefficients Standard Error t Stat P-value Intercept 0.3130 0.5144 0.6085 0.5509 XLag1 1.1737 0.2465 4.7617 0.0002 XLag2 -0.0694 0.3731 -0.1860 0.8547 XLag3 -0.1221 0.2820 -0.4330 0.6704 -Referring to Scenario 16-9 and using a 5% level of significance, what is the appropriate autoregressive model for the company's real operating revenue?

SCENARIO 16-9 Given below are EXCEL outputs for various estimated autoregressive models for a company's real operating revenues (in billions of dollars) from 1989 to 2012. From the data, you also know that the real operating revenues for 2010, 2011, and 2012 are 11.7909, 11.7757 and 11.5537, respectively. First-Order Autoregressive Model: Coefficients Standard Eiror t Stat P -value Intercept 0.1802 0.3980 0.4528 0.6553 XLag1 1.0112 0.0497 20.3526 0.0000 Second-Order Autoregressive Model: Coefficients Standard Error t Stat P -value Intercept 0.3005 0.4408 0.6817 0.5036 X Lag 1 1.1732 0.2347 4.9980 0.0001 X Lag 2 -0.1830 0.2507 -0.7300 0.4743 Third-Order Autoregressive Model: Coefficients Standard Error t Stat P-value Intercept 0.3130 0.5144 0.6085 0.5509 XLag1 1.1737 0.2465 4.7617 0.0002 XLag2 -0.0694 0.3731 -0.1860 0.8547 XLag3 -0.1221 0.2820 -0.4330 0.6704 -Referring to Scenario 16-9, if one decides to use the Third-Order Autoregressive model , what will the predicted real operating revenue for the company be in 2015?

SCENARIO 16-12 A local store developed a multiplicative time-series model to forecast its revenues in future quarters, using quarterly data on its revenues during the 5-year period from 2009 to 2013. The following is the resulting regression equation: $\log _ { 10 } \hat { Y } = 6.102 + 0.012 X - 0.129 Q _ { 1 } - 0.054 Q _ { 2 } + 0.098 Q _ { 3 }$ where $\hat { Y }$ is the estimated number of contracts in a quarter $X$ is the coded quarterly value with $X = 0$ in the first quarter of 2008 . $Q _ { 1 }$ is a dummy variable equal to 1 in the first quarter of a year and 0 otherwise. $Q _ { 2 }$ is a dummy variable equal to 1 in the second quarter of a year and 0 otherwise. $Q _ { 3 }$ is a dummy variable equal to 1 in the third quarter of a year and 0 otherwise. -Referring to Scenario 16-12, the best interpretation of the coefficient of Q3 (0.098) in the regression equation is:

SCENARIO 16-15-A You are the CEO of a diary company. The total milk production (in gallons) from your company over the past 30 years are presented below and also contained in the Excel file SCENARIO 16- 15-A.XLSX. Year 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 Milk 150201 172719 171357 157121 155727 152974 153443 158548 162614 164210 Prod 159127 153866 165992 177843 167477 163821 161700 170348 174105 185103 184670 173385 159695 173641 165706 171164 168706 150684 179314 163802 You want to predict your company's future total milk production using the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model. -Referring to Scenario 16-15-A, what is your forecast for 2016 using the third-order autoregressive model?

SCENARIO 16-13 Given below is the monthly time series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the 1st month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 $\text { Quadratic trend model: }$ $\text { Exponential trend model: }$ Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 -Referring to Scenario 16-13, what is the exponentially smoothed forecast for the $13 ^ { \text {th } }$ month using a smoothing coefficient of W = 0.5 if the exponentially smooth value for the $10 ^ { \text {th } }$ and $11 ^ { \text {th } }$ month are 9,746.3672 and 9,480.1836, respectively?

The annual multiplicative time-series model does not possess _______ component.

SCENARIO 16-2 The monthly advertising expenditures of a department store chain (in $1,000,000s) were collected over the last decade. The last 14 months of this time series follows: $\begin{array} { c l } \text { Month } & \text { Expenditures (\$) } \\\hline 1 & 1.4 \\2 & 1.8 \\3 & 1.6 \\4 & 1.5 \\5 & 1.8 \\6 & 1.7 \\7 & 1.9 \\8 & 2.2 \\9 & 1.9 \\10 & 1.9 \\11 & 2.1 \\12 & 2.4 \\13 & 2.8 \\14 & 3.1\end{array}$ -Referring to Scenario 16-2, set up a scatter plot (i.e., time-series plot) with months on the horizontal X-axis.

SCENARIO 16-8 The manager of a marketing consulting firm has been examining his company's yearly profits. He believes that these profits have been showing a quadratic trend since 1994. He uses Microsoft Excel to obtain the partial output below. The dependent variable is profit (in thousands of dollars), while the independent variables are coded years and squared of coded years, where 1994 is coded as 0, 1995 is coded as 1, etc. 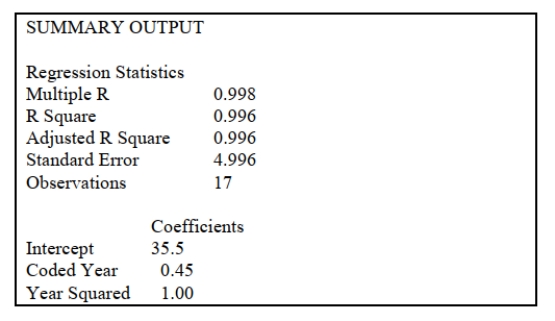-Referring to Scenario 16-8, the fitted value for 1999 is __________.

SCENARIO 16-15-B You are the CEO of a diary company. The total milk production (in gallons) from your company over the past 30 years are presented below and also contained in the Excel file SCENARIO 16- 15-B.XLSX. Year 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 Milk 150201 193718 212520 214553 237507 248069 241824 234627 252049 252029 Prod 263449 260689 247900 260059 268197 249477 246216 265236 256364 241705 245932 243529 241551 247697 248454 241974 235823 243517 238490 248606 You want to predict your company's future total milk production using the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model. -Referring to Scenario 16-15-B, what is your forecast for 2016 using the quadratic-trend model?