Exam 5: Inverse, Exponential, and Logarithmic Functions
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
Use properties of logarithms to evaluate the expression.
-
(Multiple Choice)
4.8/5  (30)
(30)
The population of a particular city is increasing at a rate proportional to its size. It follows the function P(t) = 1 + ke0.08t where k is a constant and t is the time in years. If the current population is 22,000, in how many
Years is the population expected to be 55,000? Round to the nearest year.
(Multiple Choice)
4.9/5  (44)
(44)
Find the value. Give an approximation to four decimal places.
-
(Multiple Choice)
4.8/5  (40)
(40)
Suppose that the salinity of ocean water at a given depth is modeled by the equation , where is measured in grams salt per kilogram water and is measured in meters. What is the salinity when the depth is ? Round your answer to the nearest hundredth.
(Multiple Choice)
4.9/5  (39)
(39)
Find the value. Give an approximation to four decimal places.
-
(Multiple Choice)
4.8/5  (33)
(33)
Provide an appropriate response.
-The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of .
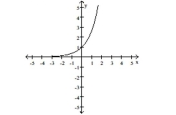
(Essay)
4.9/5  (34)
(34)
An earthquake was recorded with an intensity which was 125,893 times more powerful than a reference level earthquake, or 125,893 · I0. What is the magnitude of this earthquake on the Richter scale (rounded to the
Nearest tenth)? Intensity on the Richter scale is log10
(Multiple Choice)
4.9/5  (35)
(35)
In the formula A(t) = A0ekt, A is the amount of radioactive material remaining from an initial amount A0 at a given time t, and k is a negative constant determined by the nature of the material. A certain radioactive isotope
Decays at a rate of 0.3% annually. Determine the half-life of this isotope, to the nearest year.
(Multiple Choice)
4.8/5  (46)
(46)
Assume the cost of a gallon of milk is $3.40. With continuous compounding, find the time it would take the cost to be 4 times as much (to the nearest tenth of a year), at an annual inflation rate of 6%.
(Multiple Choice)
4.9/5  (32)
(32)
Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.7/5  (41)
(41)
The decay of 243 mg of an isotope is given by where t is time in years since the initial amount of 243 mg was present. Find the amount (to the nearest milligram) left after 72 years.
(Multiple Choice)
4.9/5  (32)
(32)
Find the value. Give an approximation to four decimal places.
-
(Multiple Choice)
4.9/5  (32)
(32)
Showing 321 - 340 of 472
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)