Question 1

Give the domain and range.
-$f(x)=\log _{2} x+4$

Accepted Answer

A)  domain: $( \infty , \infty )$; range: $( 4 , \infty )$
  
B)  domain: $( 0 , \infty )$; range: $( \infty , \infty )$
  
C)  domain: $( - 4 , \infty )$; range: $( \infty , 0 )$
  
D)  domain: $( \infty , 0 )$; range: $( \infty , \infty )$
  
A)  domain: $( \infty , \infty )$; range: $( 4 , \infty )$
  
B)  domain: $( 0 , \infty )$; range: $( \infty , \infty )$
  
C)  domain: $( - 4 , \infty )$; range: $( \infty , 0 )$
  
D)  domain: $( \infty , 0 )$; range: $( \infty , \infty )$

Question 2

Find the value. Give an approximation to four decimal places.
-$\ln \left( \frac { 102 } { 15 } \right)$

Accepted Answer

A)  $1.7079$ 
B)  $1.9169$ 
C)  $7.3330$ 
D)  $- 2.1531$ 
A)  $1.7079$ 
B)  $1.9169$ 
C)  $7.3330$ 
D)  $- 2.1531$

Question 3

What are the domain and range for the equation $y = 2 ^ { x }$ ?

Accepted Answer

A)  Domain: $( -\infty , \infty )$; range: $( -\infty , \infty )$ 
B)  $( -\infty , \infty )$; range: $[ 0 , \infty )$ 
C)  Domain: $( 0 , \infty )$; range: $( -\infty , \infty )$ 
D)  Domain: $( -\infty , \infty )$; range: $( 0 , \infty )$ 
A)  Domain: $( -\infty , \infty )$; range: $( -\infty , \infty )$ 
B)  $( -\infty , \infty )$; range: $[ 0 , \infty )$ 
C)  Domain: $( 0 , \infty )$; range: $( -\infty , \infty )$ 
D)  Domain: $( -\infty , \infty )$; range: $( 0 , \infty )$

Question 4

Give the domain and range.
-$$f ( x ) = \log _ { 4 } ( x + 4 )$$

Accepted Answer

A)  domain: $( 0 , \infty )$; range: $( \infty , \infty )$
  
B)  domain: $( \infty , \infty )$; range: $( 4 , \infty )$
  
C)  domain: $( \infty , \infty )$; range: $( 0 , \infty )$
  
D)  domain: $( - 4 , \infty )$; range: $( \infty , \infty )$
  
A)  domain: $( 0 , \infty )$; range: $( \infty , \infty )$
  
B)  domain: $( \infty , \infty )$; range: $( 4 , \infty )$
  
C)  domain: $( \infty , \infty )$; range: $( 0 , \infty )$
  
D)  domain: $( - 4 , \infty )$; range: $( \infty , \infty )$

Question 5

Determine whether or not the function is one-to-one.
-$f ( x ) = \left| 9 - x ^ { 2 } \right|$

Accepted Answer

A) True 
 B)False

Question 6

Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent positive real numbers.
-$\log _ { 2 } \left( \frac { x ^ { 9 } y ^ { 7 } } { 7 } \right)$

Accepted Answer

A)  $9 \log _ { 2 } x + 7 \log 2 y - \log _ { 2 } 7$ 
B)  $\left( 9 \log _ { 2 } x \right) \left( 7 \log _ { 2 } y \right) \div \log _ { 2 } 7$ 
C)  $\left( \log _ { 2 } x \right) ^ { 9 } + \left( \log _ { 2 } y \right) ^ { 7 } - \log _ { 2 } 7$ 
D)  $9 \log _ { 2 } x + 7 \log 2 y + \log _ { 2 } 7$ 
A)  $9 \log _ { 2 } x + 7 \log 2 y - \log _ { 2 } 7$ 
B)  $\left( 9 \log _ { 2 } x \right) \left( 7 \log _ { 2 } y \right) \div \log _ { 2 } 7$ 
C)  $\left( \log _ { 2 } x \right) ^ { 9 } + \left( \log _ { 2 } y \right) ^ { 7 } - \log _ { 2 } 7$ 
D)  $9 \log _ { 2 } x + 7 \log 2 y + \log _ { 2 } 7$

Question 7

Explain the error in the following: $$\log _ { 6 } 8 - \log _ { 6 } N = \log _ { 6 } ( 8 - N )$$

Accepted Answer

A difference of logarithms is

Question 8

Solve the equation.
-$$2^{ ( 5 + 3 x )} = \frac { 1 } { 16 }$$

Accepted Answer

A)  $\{ 3 \}$ 
B)  $\{ - 3 \}$ 
C)  $\left\{ \frac { 1 } { 8 } \right\}$ 
D)  $\{ 4 \}$ 
A)  $\{ 3 \}$ 
B)  $\{ - 3 \}$ 
C)  $\left\{ \frac { 1 } { 8 } \right\}$ 
D)  $\{ 4 \}$

Question 9

The population of country A in millions is modeled by $f ( x ) = 16.8 \mathrm { e } ^ { 0.0019 x }$. During the same time period, the population of country B in millions is modeled by $g ( x ) = 13.3 e ^ { 0.0124 x }$. In both formulas $x$ is the number of years. Assuming these trends continue, estimate what the population will be when the populations are equal. Round to the nearest million.

Accepted Answer

A)  16 million 
B)  18 million 
C)  17 million 
D)  1 million 
A)  16 million 
B)  18 million 
C)  17 million 
D)  1 million

Question 10

Determine whether or not the function is one-to-one.
-

Accepted Answer

A) True 
 B)False

Question 11

Use the definition of inverses to determine whether f and g are inverses.
-$f ( x ) = \frac { 1 } { x + 2 } , \quad g ( x ) = \frac { 2 x + 1 } { x }$

Accepted Answer

A) True 
 B)False

Question 12

Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent positive real numbers.
-$\log 8 \left( \frac { \sqrt { 11 } } { 12 } \right)$

Accepted Answer

A)  $\frac { 1 } { 2 } \log 811 - \log _ { 8 } 12$ 
B)  $\log 8 \sqrt { 11 } + \log 812$ 
C)  $\frac { \frac { 1 } { 2 } \log _ { 8 } 11 } { \log _ { 8 } 12 }$ 
D)  $\sqrt { \log _ { 8 } 11 } - \log _ { 8 } 12$ 
A)  $\frac { 1 } { 2 } \log 811 - \log _ { 8 } 12$ 
B)  $\log 8 \sqrt { 11 } + \log 812$ 
C)  $\frac { \frac { 1 } { 2 } \log _ { 8 } 11 } { \log _ { 8 } 12 }$ 
D)  $\sqrt { \log _ { 8 } 11 } - \log _ { 8 } 12$

Question 13

Solve the following graphically. If necessary, round answers to the nearest thousandth.
-$$\mathrm { e } ^ { \mathrm { x } + 1 } = \frac { 1 } { \mathrm { x } + 3 }$$

Accepted Answer

A)  $\{ - 1.443 \}$ 
B)  $\varnothing$ 
C)  $\{ - 4.5981 , - 1.4756 \}$ 
D)  $\{ - 3.000 , - 1.443 \}$ 
A)  $\{ - 1.443 \}$ 
B)  $\varnothing$ 
C)  $\{ - 4.5981 , - 1.4756 \}$ 
D)  $\{ - 3.000 , - 1.443 \}$

Question 14

Coffee is best enjoyed at a temperature of 118°F. A restaurant owner wants to discover the temperature T at which he should serve his coffee so that it will have cooled to this ideal temperature in 4 minutes. He discovers
That a cup of coffee served at 197°F cools to 184°F in one minute when his restaurant is at 68°F. If he maintains
The restaurant temperature at 68°F, at what temperature should he serve the coffee to meet his goal?

Accepted Answer

A)  144°F 
B)  139°F 
C)  164°F 
D)  197°F 
A)  144°F 
B)  139°F 
C)  164°F 
D)  197°F

Question 15

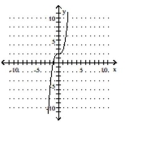
Use the graph of f to sketch a graph of the inverse of f using a dashed curve.
-

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 16

Write the expression as a single logarithm with coefficient 1. Assume all variables represent positive real numbers with $a \neq 1 \text { and } b \neq 1$ .
-$$\frac { 3 } { 4 } \log _ { a } \left( p ^ { 2 } q ^ { 8 } \right) - \frac { 1 } { 2 } \log _ { a } \left( p ^ { 5 } q ^ { 2 } \right)$$

Accepted Answer

A)  $\log _ { a } \left( p ^ { 4 } q ^ { 7 } \right)$ 
B)  $\log _ { a } \left( \frac { 3 } { 4 } p ^ { 2 } q ^ { 8 } - \frac { 1 } { 2 } p ^ { 5 } q ^ { 2 } \right)$ 
C)  $\log _ { a } \left( \frac { 3 q ^ { 6 } } { 2 p ^ { 3 } } \right)$ 
D)  $\log _ { a } \left( \frac { q ^ { 5 } } { p } \right)$ 
A)  $\log _ { a } \left( p ^ { 4 } q ^ { 7 } \right)$ 
B)  $\log _ { a } \left( \frac { 3 } { 4 } p ^ { 2 } q ^ { 8 } - \frac { 1 } { 2 } p ^ { 5 } q ^ { 2 } \right)$ 
C)  $\log _ { a } \left( \frac { 3 q ^ { 6 } } { 2 p ^ { 3 } } \right)$ 
D)  $\log _ { a } \left( \frac { q ^ { 5 } } { p } \right)$

Question 17

Match the function with its graph.
-$$f ( x ) = \log _ { 6 } x$$

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 18

Write the expression as a single logarithm with coefficient 1. Assume all variables represent positive real numbers with $a \neq 1 \text { and } b \neq 1$ .
-$3 \log _ { a } x - 9 \log _ { a } z ^ { 2 }$

Accepted Answer

A)  $\frac { \log _ { a } x ^ { 3 } } { \log _ { a } z ^ { 18 } }$ 
B)  $\log _ { a } \left( \frac { x ^ { 3 } } { z ^ { 11 } } \right)$ 
C)  $\log _ { a } \left( \frac { x ^ { 3 } } { z ^ { 18 } } \right)$ 
D)  $\log _ { a } \left( \frac { 3 x } { 9 z ^ { 2 } } \right)$ 
A)  $\frac { \log _ { a } x ^ { 3 } } { \log _ { a } z ^ { 18 } }$ 
B)  $\log _ { a } \left( \frac { x ^ { 3 } } { z ^ { 11 } } \right)$ 
C)  $\log _ { a } \left( \frac { x ^ { 3 } } { z ^ { 18 } } \right)$ 
D)  $\log _ { a } \left( \frac { 3 x } { 9 z ^ { 2 } } \right)$

Question 19

Find the value. Give an approximation to four decimal places.
-$\ln \left( 6.09 \times \mathrm { e } ^ { 3 } \right)$

Accepted Answer

A)  $- 1.1934$ 
B)  $3.2648$ 
C)  $4.8066$ 
D)  $1.8066$ 
A)  $- 1.1934$ 
B)  $3.2648$ 
C)  $4.8066$ 
D)  $1.8066$

Question 20

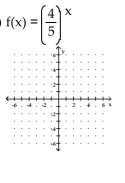
Find the function value. If the result is irrational, round your answer to the nearest thousandth.
-

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Give the domain and range. - $f(x)=\log _{2} x+4$ $Give the domain and range. - f(x)=\log _{2} x+4$

Find the value. Give an approximation to four decimal places. - $\ln \left( \frac { 102 } { 15 } \right)$

What are the domain and range for the equation $y = 2 ^ { x }$ ?

Give the domain and range. - $f ( x ) = \log _ { 4 } ( x + 4 )$ $Give the domain and range. - f ( x ) = \log _ { 4 } ( x + 4 )$

Determine whether or not the function is one-to-one. - $f ( x ) = \left| 9 - x ^ { 2 } \right|$

Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent positive real numbers. - $\log _ { 2 } \left( \frac { x ^ { 9 } y ^ { 7 } } { 7 } \right)$

Explain the error in the following: $\log _ { 6 } 8 - \log _ { 6 } N = \log _ { 6 } ( 8 - N )$

Solve the equation. - $2^{ ( 5 + 3 x )} = \frac { 1 } { 16 }$

Determine whether or not the function is one-to-one. -

Use the definition of inverses to determine whether f and g are inverses. - $f ( x ) = \frac { 1 } { x + 2 } , \quad g ( x ) = \frac { 2 x + 1 } { x }$

Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent positive real numbers. - $\log 8 \left( \frac { \sqrt { 11 } } { 12 } \right)$

Solve the following graphically. If necessary, round answers to the nearest thousandth. - $\mathrm { e } ^ { \mathrm { x } + 1 } = \frac { 1 } { \mathrm { x } + 3 }$

Use the graph of f to sketch a graph of the inverse of f using a dashed curve. -

Write the expression as a single logarithm with coefficient 1. Assume all variables represent positive real numbers with $a \neq 1 \text { and } b \neq 1$ . - $\frac { 3 } { 4 } \log _ { a } \left( p ^ { 2 } q ^ { 8 } \right) - \frac { 1 } { 2 } \log _ { a } \left( p ^ { 5 } q ^ { 2 } \right)$

Match the function with its graph. - $f ( x ) = \log _ { 6 } x$

Write the expression as a single logarithm with coefficient 1. Assume all variables represent positive real numbers with $a \neq 1 \text { and } b \neq 1$ . - $3 \log _ { a } x - 9 \log _ { a } z ^ { 2 }$

Find the value. Give an approximation to four decimal places. - $\ln \left( 6.09 \times \mathrm { e } ^ { 3 } \right)$

Find the function value. If the result is irrational, round your answer to the nearest thousandth. -

Review of Basic Concepts

Equations and Inequalities

Graphs and Functions

Polynomials and Rational Functions

Systems and Matrices

Arithmetic Sequence: Common Difference and First n Terms

Filters

Exam 5: Inverse, Exponential, and Logarithmic Functions

Give the domain and range. - f(x)=log⁡2x+4f(x)=\log _{2} x+4f(x)=log2​x+4

Find the value. Give an approximation to four decimal places. - ln⁡(10215)\ln \left( \frac { 102 } { 15 } \right)ln(15102​)

What are the domain and range for the equation y=2xy = 2 ^ { x }y=2x ?

Give the domain and range. - f(x)=log⁡4(x+4)f ( x ) = \log _ { 4 } ( x + 4 )f(x)=log4​(x+4)

Determine whether or not the function is one-to-one. - f(x)=∣9−x2∣f ( x ) = \left| 9 - x ^ { 2 } \right|f(x)=​9−x2​

Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent positive real numbers. - log⁡2(x9y77)\log _ { 2 } \left( \frac { x ^ { 9 } y ^ { 7 } } { 7 } \right)log2​(7x9y7​)

Explain the error in the following: log⁡68−log⁡6N=log⁡6(8−N)\log _ { 6 } 8 - \log _ { 6 } N = \log _ { 6 } ( 8 - N )log6​8−log6​N=log6​(8−N)

Solve the equation. - 2(5+3x)=1162^{ ( 5 + 3 x )} = \frac { 1 } { 16 }2(5+3x)=161​

Determine whether or not the function is one-to-one. -

Use the definition of inverses to determine whether f and g are inverses. - f(x)=1x+2,g(x)=2x+1xf ( x ) = \frac { 1 } { x + 2 } , \quad g ( x ) = \frac { 2 x + 1 } { x }f(x)=x+21​,g(x)=x2x+1​

Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent positive real numbers. - log⁡8(1112)\log 8 \left( \frac { \sqrt { 11 } } { 12 } \right)log8(1211​​)

Solve the following graphically. If necessary, round answers to the nearest thousandth. - ex+1=1x+3\mathrm { e } ^ { \mathrm { x } + 1 } = \frac { 1 } { \mathrm { x } + 3 }ex+1=x+31​

Use the graph of f to sketch a graph of the inverse of f using a dashed curve. -

Match the function with its graph. - f(x)=log⁡6xf ( x ) = \log _ { 6 } xf(x)=log6​x

Write the expression as a single logarithm with coefficient 1. Assume all variables represent positive real numbers with a≠1 and b≠1a \neq 1 \text { and } b \neq 1a=1 and b=1 . - 3log⁡ax−9log⁡az23 \log _ { a } x - 9 \log _ { a } z ^ { 2 }3loga​x−9loga​z2

Find the value. Give an approximation to four decimal places. - ln⁡(6.09×e3)\ln \left( 6.09 \times \mathrm { e } ^ { 3 } \right)ln(6.09×e3)

Find the function value. If the result is irrational, round your answer to the nearest thousandth. -

Review of Basic Concepts

Equations and Inequalities

Graphs and Functions

Polynomials and Rational Functions

Systems and Matrices

Arithmetic Sequence: Common Difference and First n Terms

Filters

Give the domain and range. - $f(x)=\log _{2} x+4$ $Give the domain and range. - f(x)=\log _{2} x+4$

Find the value. Give an approximation to four decimal places. - $\ln \left( \frac { 102 } { 15 } \right)$

What are the domain and range for the equation $y = 2 ^ { x }$ ?

Give the domain and range. - $f ( x ) = \log _ { 4 } ( x + 4 )$ $Give the domain and range. - f ( x ) = \log _ { 4 } ( x + 4 )$

Determine whether or not the function is one-to-one. - $f ( x ) = \left| 9 - x ^ { 2 } \right|$

Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent positive real numbers. - $\log _ { 2 } \left( \frac { x ^ { 9 } y ^ { 7 } } { 7 } \right)$

Explain the error in the following: $\log _ { 6 } 8 - \log _ { 6 } N = \log _ { 6 } ( 8 - N )$

Solve the equation. - $2^{ ( 5 + 3 x )} = \frac { 1 } { 16 }$

Use the definition of inverses to determine whether f and g are inverses. - $f ( x ) = \frac { 1 } { x + 2 } , \quad g ( x ) = \frac { 2 x + 1 } { x }$

Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent positive real numbers. - $\log 8 \left( \frac { \sqrt { 11 } } { 12 } \right)$

Solve the following graphically. If necessary, round answers to the nearest thousandth. - $\mathrm { e } ^ { \mathrm { x } + 1 } = \frac { 1 } { \mathrm { x } + 3 }$

Match the function with its graph. - $f ( x ) = \log _ { 6 } x$

Write the expression as a single logarithm with coefficient 1. Assume all variables represent positive real numbers with $a \neq 1 \text { and } b \neq 1$ . - $3 \log _ { a } x - 9 \log _ { a } z ^ { 2 }$

Find the value. Give an approximation to four decimal places. - $\ln \left( 6.09 \times \mathrm { e } ^ { 3 } \right)$