Exam 5: Inverse, Exponential, and Logarithmic Functions
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
For the function as defined that is one-to-one, graph f and on the same axes.
-
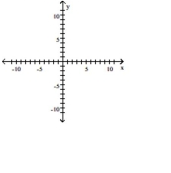
(Multiple Choice)
4.8/5  (40)
(40)
Use the definition of inverses to determine whether f and g are inverses.
-
(True/False)
4.9/5  (33)
(33)
Write the expression as a single logarithm with coefficient 1. Assume all variables represent positive real numbers with .
-
(Multiple Choice)
4.9/5  (33)
(33)
An everyday activity is described. Keeping in mind that an inverse operation "undoes" what an operation does, describe each inverse activity.
-setting a clock forward by one hour
(Multiple Choice)
4.8/5  (36)
(36)
Use a graphing calculator to estimate the solution set of the equation. Round to the nearest hundredth.
-
(Multiple Choice)
4.8/5  (38)
(38)
If an earthquake measured on the Richter scale, what was the approximate intensity of the earthquake in terms of IO? Intensity on the Richter scale is .
(Multiple Choice)
4.9/5  (32)
(32)
Find the value. Give an approximation to four decimal places.
-log 4176
(Multiple Choice)
4.9/5  (41)
(41)
Find the function value. If the result is irrational, round your answer to the nearest thousandth.
-
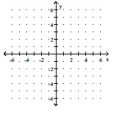
(Multiple Choice)
4.8/5  (23)
(23)
Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (37)
(37)
The hydrogen potential, , of a substance is defined by , where is measured in moles per liter. Find the pH of a sample of lake water whose is moles per liter. (Round to the nearest tenth.)
(Multiple Choice)
4.8/5  (45)
(45)
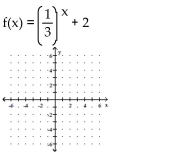
Graph the exponential function using transformations where appropriate.
-
(Multiple Choice)
4.9/5  (27)
(27)
Decide whether the given functions are inverses.
- f=\{(4,8),(8,-2),(-2,-7)\} g=\{(8,4),(-2,8),(-7,4)\}
(True/False)
4.8/5  (26)
(26)
Determine whether the statement is true or false.
-If f is a one-to-one function and the graph of f lies completely within the second quadrant, then the graph of lies completely within the fourth quadrant.
(True/False)
4.8/5  (35)
(35)
Showing 341 - 360 of 472
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)