Exam 5: Inverse, Exponential, and Logarithmic Functions
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
Round your answer to the nearest tenth, when appropriate. Use the formula , as
needed.
-Find if the .
(Multiple Choice)
4.8/5  (40)
(40)
The graph of a function f is given. Use the graph to find the indicated value.
-
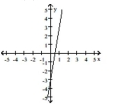
(Multiple Choice)
4.7/5  (28)
(28)
Determine whether the statement is true or false.
-If a function f has an inverse, then the graph of can be obtained by reflecting the graph of f across the x-axis.
(True/False)
4.8/5  (41)
(41)
Solve the equation and express the solution in exact form.
-
(Multiple Choice)
4.7/5  (34)
(34)
Solve the equation and express the solution in exact form.
-
(Multiple Choice)
4.8/5  (44)
(44)
Decide whether the given functions are inverses.
- f=\{(-3,-6),(0,4),(4,-3),(8,10)\} g=\{(-6,-3),(4,0),(-3,4),(10,8)\}
(True/False)
4.8/5  (37)
(37)
Find the function value. If the result is irrational, round your answer to the nearest thousandth.
-
(Multiple Choice)
4.9/5  (39)
(39)
In the formula N , N is the number of items in terms of an initial population I at a given time t and k is a growth constant equal to the percent of growth per unit time. How long will it take for the population of a
Certain country to triple if its annual growth rate is 5.7%? Round to the nearest year.
(Multiple Choice)
4.9/5  (30)
(30)
Write the expression as a single logarithm with coefficient 1. Assume all variables represent positive real numbers with .
-
(Multiple Choice)
4.8/5  (35)
(35)
Provide an appropriate response.
-Give an equation of the form to define the exponential function whose graph contains the point . Assume that .
(Multiple Choice)
4.9/5  (40)
(40)
Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.9/5  (36)
(36)
Use a graphing calculator to estimate the solution set of the equation. Round to the nearest hundredth.
-
(Multiple Choice)
4.7/5  (41)
(41)
If the function is one-to-one, find its inverse. If not, write "not one-to-one."
-
(Multiple Choice)
4.8/5  (34)
(34)
Use a graphing calculator to estimate the solution set of the equation. Round to the nearest hundredth.
-
(Multiple Choice)
4.9/5  (28)
(28)
Showing 441 - 460 of 472
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)