Exam 15: Graph Theory
Exam 1: The Art of Problem Solving190 Questions
Exam 2: The Basic Concepts of Set Theory316 Questions
Exam 3: Introduction to Logic315 Questions
Exam 4: Numeration Systems245 Questions
Exam 5: Number Theory171 Questions
Exam 6: The Real Numbers and Their Representations401 Questions
Exam 7: The Basic Concepts of Algebra273 Questions
Exam 8: Graphs, Functions, and Systems of Equations and Inequalities136 Questions
Exam 9: Geometry182 Questions
Exam 10: Counting Methods213 Questions
Exam 11: Probability140 Questions
Exam 12: Statistics152 Questions
Exam 13: Personal Financial Management260 Questions
Exam 14: Trigonometry Formerly234 Questions
Exam 15: Graph Theory110 Questions
Exam 16: Voting and Apportionment99 Questions
Select questions type
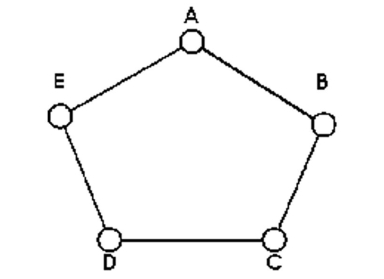
Determine whether the sequence of vertices is an Euler circuit.
-
(Multiple Choice)
5.0/5  (29)
(29)
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
-A graph with 7 vertices, one of degree 4, three of degree 3, and three of degree 1.
(Multiple Choice)
4.7/5  (39)
(39)
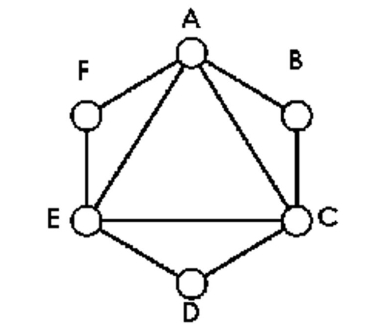
Determine whether the sequence of vertices is an Euler circuit.
-
(Multiple Choice)
4.8/5  (37)
(37)
Determine whether the two graphs are isomorphic. If they are, illustrate the isomorphism.
-(a)
 (b)
(b)

(Essay)
4.8/5  (37)
(37)
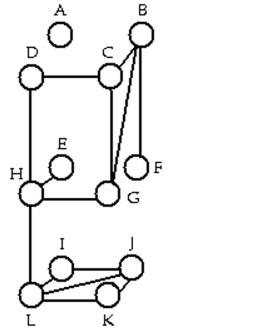
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.
-
(Multiple Choice)
4.8/5  (42)
(42)
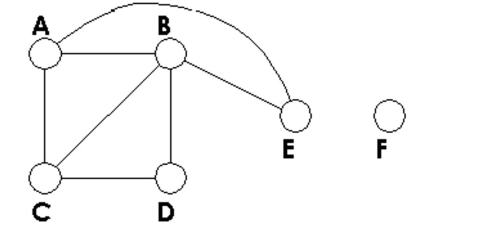
Determine how many vertices and how many edges the graph has.
-
(Multiple Choice)
4.8/5  (35)
(35)
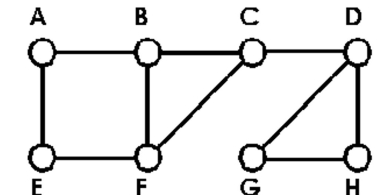
Identify the cut edges in the graph or say there are none.
-
(Multiple Choice)
4.7/5  (38)
(38)
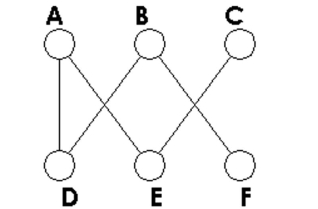
Determine how many vertices and how many edges the graph has.
-
(Multiple Choice)
4.8/5  (39)
(39)
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
-A graph with 6 vertices, one of degree 5, three of degree 1, and two of degree 2.
(Multiple Choice)
5.0/5  (39)
(39)
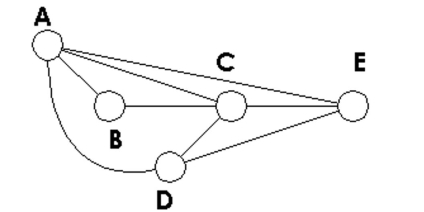
Determine how many vertices and how many edges the graph has.
-
(Multiple Choice)
4.9/5  (31)
(31)
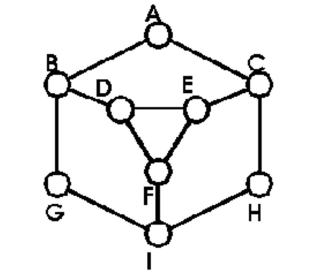
Identify the cut edges in the graph or say there are none.
-
(Multiple Choice)
4.8/5  (35)
(35)
Showing 21 - 40 of 110
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)