Exam 15: Graph Theory
Exam 1: The Art of Problem Solving190 Questions
Exam 2: The Basic Concepts of Set Theory316 Questions
Exam 3: Introduction to Logic315 Questions
Exam 4: Numeration Systems245 Questions
Exam 5: Number Theory171 Questions
Exam 6: The Real Numbers and Their Representations401 Questions
Exam 7: The Basic Concepts of Algebra273 Questions
Exam 8: Graphs, Functions, and Systems of Equations and Inequalities136 Questions
Exam 9: Geometry182 Questions
Exam 10: Counting Methods213 Questions
Exam 11: Probability140 Questions
Exam 12: Statistics152 Questions
Exam 13: Personal Financial Management260 Questions
Exam 14: Trigonometry Formerly234 Questions
Exam 15: Graph Theory110 Questions
Exam 16: Voting and Apportionment99 Questions
Select questions type
Use Fleury's algorithm to find an Euler circuit for the graph beginning and ending at the indicated vertex. If no Euler
circuit exists, state this.
-Using the following graph, find an Euler circuit that begins and ends with vertex A.
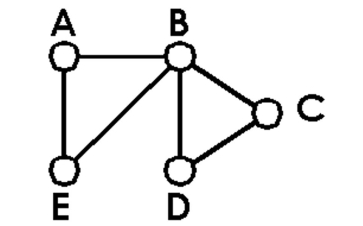
(Multiple Choice)
4.7/5  (35)
(35)
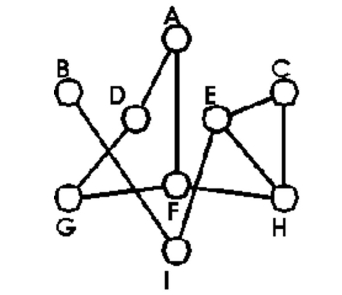
Identify the cut edges in the graph or say there are none.
-
(Multiple Choice)
4.9/5  (42)
(42)
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
-A graph with 7 vertices, one of degree 6 and six of degree 1.
(Multiple Choice)
4.8/5  (38)
(38)
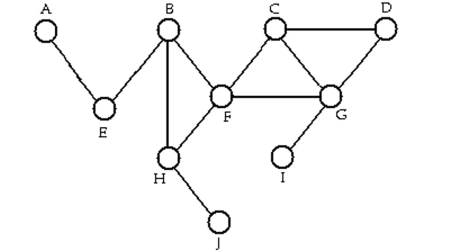
Determine whether the sequence of vertices is i)a walk, ii)a path, iii)a circuit in the given graph.
-
(Multiple Choice)
4.9/5  (40)
(40)
Determine whether the two graphs are isomorphic. If they are, illustrate the isomorphism.
-(a)
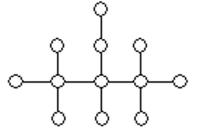 (b)
(b)
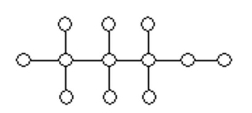
(Essay)
4.8/5  (30)
(30)
Solve the problem.
-Two schools play a tennis tournament. Each school has a team made up of 5 players, and
each player must play one match with each player of the opposing team. Draw a graph
with vertices representing players and edges representing matches. How many matches
will be played in the tournament?
(Essay)
4.8/5  (32)
(32)
Use the theorem that relates the sum of degrees to the number of edges to determine the number of edges in the graph.
-A graph with 8 vertices, two of degree 2, four of degree 3, and two of degree 1.
(Multiple Choice)
4.7/5  (42)
(42)
Showing 101 - 110 of 110
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)