Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function

Find the limit as x approaches c of the average rate of change of the function from c to x. -c = -3; $f ( x ) = 2 x ^ { 2 } + 3$

Find the numbers at which f is continuous. At which numbers is f discontinuous? - $f ( x ) = \left\{ \begin{aligned}7 x & \text { if } x < 6 \\41 & \text { if } x = 6 \\x ^ { 2 } + 6 & \text { if } x > 6\end{aligned} \right.$

Solve the problem. -An explosion causes debris to rise vertically with an initial velocity of 112 feet per second. The function $s ( t ) = - 16 t ^ { 2 } + 112 t$ describes the height of the debris above the ground, s(t), in feet, t seconds after the explosion. What is the instantaneous speed of the debris when it hits the ground?

Use the graph of y = g(x) to answer the question. 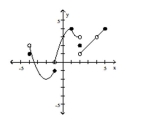-Find f(-1).

Choose the one alternative that best completes the statement or answers the question. Find the slope of the tangent line to the graph at the given point. - $f ( x ) = 2 x - 9 \text { at } ( 8,7 )$

Solve the problem. - $\mathrm { f } ( \mathrm { x } ) = \sqrt { \mathrm { x } ^ { 2 } + 1 }$ is defined on the interval $[ 0,4 ]$ . In (a) and (b), approximate the area under $\mathrm { f }$ (to three decimal place follows: (a) Partition $[ 0,4 ]$ into four subintervals of equal length and choose $u$ as the left endpoint of each subinterval. (b) Partition $[ 0,4 ]$ into four subintervals of equal length and choose $\mathrm { u }$ as the right endpoint of each subinterval. (c) Use a graphing utility to approximate the actual area $A$ . s

Find the equation of the tangent line to the graph of f at the given point. - $f ( x ) = 2 x ^ { 2 } + x - 3 \text { at } x = ( 4,33 )$

Determine whether f is continuous at c. - $f ( x ) = \frac { x ^ { 2 } - 36 } { x - 6 } ; \quad c = 6$

Use the TABLE feature of a graphing utility to find the limit. - $\lim _ { x \rightarrow 2 } \left( x ^ { 2 } + 8 x - 2 \right)$

Use the graph of y = g(x) to answer the question. -Find the y-intercept(s), if any, of g.

Find the equation of the tangent line to the graph of f at the given point. - $f ( x ) = x ^ { 2 } + 5 x \text { at } ( 4,20 )$

Solve the problem. -The volume of a right cylindrical cone of height $6 \mathrm {~cm}$ and radius $\mathrm { r } \mathrm { cm }$ is $\mathrm { V } ( \mathrm { r } ) = 2 \pi \mathrm { r } ^ { 2 } \mathrm { cubic }$ centimeters (cm 3 ). Find the instantaneous rate of change of the volume with respect to the radius $r$ when $r = 4 \mathrm {~cm}$ .

Find the limit algebraically. - $\lim _ { x \rightarrow0 } \frac { x ^ { 3 } - 6 x + 8 } { x - 2 }$

Use a graphing utility to find the indicated limit rounded to two decimal places. - $\lim _ { x \rightarrow - 1 } \frac { x ^ { 3 } - x ^ { 2 } + 3 x - 3 } { x ^ { 4 } - x ^ { 3 } + x - 1 }$

Find the numbers at which f is continuous. At which numbers is f discontinuous? - $f ( x ) = 3 x - 1$

Solve the problem. -The volume of a rectangular box with square base and a height of 5 feet is $V ( x ) = 5 x ^ { 2 }$ , where $x$ is the length of a side of the base. Find the instantaneous rate of change of volume with respect to $x$ when $x = 3$ feet.

Find the derivative of the function at the given value of x using a graphing utility. If necessary, round to four decimal places. - $f ( x ) = 4 x ^ { 3 } - 6 x + 2 ; x = - 4$

Find the derivative of the function at the given value of x. -f(x) = -7x + 11; x = 6

Write the word or phrase that best completes each statement or answers the question. -f(x) = 2x - 2 is defined on the interval 1,5 . In (a) and (b), approximate the area under f as follows: (a) Partition 1,5 into four subintervals of equal length and choose u as the left endpoint of each subinterval. (b) Partition 1,5 into four subintervals of equal length and choose u as the right endpoint of each subinterval. (c) What is the actual area A?

Use the grid to graph the function. Find the limit, if it exists - $\lim _ { x \rightarrow 8 } f ( x ) , \quad f ( x ) = 1 - x ^ { 2 }$