Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Use the TABLE feature of a graphing utility to find the limit.
-
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-An explosion causes debris to rise vertically with an initial velocity of 96 feet per second. The function describes the height of the debris above the ground, s(t), in feet, t seconds after the explosion. What is the instantaneous speed of the debris 4.8 second(s) after the explosion?
(Multiple Choice)
4.8/5  (39)
(39)
Choose the one alternative that best completes the statement or answers the question.
Find the slope of the tangent line to the graph at the given point.
-
(Multiple Choice)
4.8/5  (30)
(30)
Use the graph of y = g(x) to answer the question. 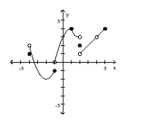 -What is the range of g? A) all real numbers
B)
C)
D)
-What is the range of g? A) all real numbers
B)
C)
D)
(Multiple Choice)
4.9/5  (41)
(41)
Use the graph of y = g(x) to answer the question.  -Find f(-4).
-Find f(-4).
(Multiple Choice)
4.8/5  (30)
(30)
Approximate the area under the curve and above the x-axis using n rectangles. Let the height of each rectangle be given
by the value of the function at the right side of the rectangle.
-
(Multiple Choice)
4.9/5  (36)
(36)
Use the graph shown to determine if the limit exists. If it does, find its value.
-
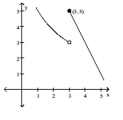
(Multiple Choice)
4.8/5  (31)
(31)
Choose the one alternative that best completes the statement or answers the question.
Find the slope of the tangent line to the graph at the given point.
-
(Multiple Choice)
4.9/5  (30)
(30)
Use the grid to graph the function. Find the limit, if it exists
-
(Multiple Choice)
4.8/5  (30)
(30)
Find the numbers at which f is continuous. At which numbers is f discontinuous?
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Given the function f defined over the interval [a, b], graph the function indicating the area A under f from a to b. Then
express the area A as an integral.
![Solve the problem. -Given the function f defined over the interval [a, b], graph the function indicating the area A under f from a to b. Then express the area A as an integral. f ( x ) = x ^ { 2 } + 3 , \quad [ - 4,2 ]](https://storage.examlex.com/TB7697/11ed86a1_f37c_7602_b056_bfffbcd46d1e_TB7697_11.jpg)
(Essay)
4.8/5  (30)
(30)
Choose the one alternative that best completes the statement or answers the question.
Find the slope of the tangent line to the graph at the given point.
-
(Multiple Choice)
4.7/5  (36)
(36)
Showing 61 - 80 of 145
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)