Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function

Solve the problem. -A foul tip of a baseball is hit straight upward from a height of 4 feet with an initial velocity of 112 feet per second. The function $s ( t ) = - 16 t ^ { 2 } + 112 t + 4$ 4 describes the ball's height above the ground, s(t), in feet, t seconds After it was hit. What is the instantaneous speed of the ball 0.5 seconds after it was hit?

Find the limit as x approaches c of the average rate of change of the function from c to x. -c = 3; f(x) = 5x + 3

Use the graph of y = g(x) to answer the question. 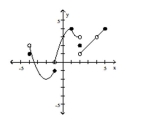-Find f(2)

Use the graph of y = g(x) to answer the question. -Does $\lim _ { x \rightarrow 4 } g ( x )$ xist? If it does, what is it?

Use the grid to graph the function. Find the limit, if it exists - $\lim _ { x \rightarrow 8 } f ( x ) , f ( x ) = 4 x - 1$

Find the limit algebraically. - $\lim _ { x \rightarrow 0 } \frac { 4 + x } { x ^ { 3 } }$

Find the numbers at which f is continuous. At which numbers is f discontinuous? - $f ( x ) = - 3 \cos x$

Find the limit algebraically. - $\lim _ { x \rightarrow 2 } \left( x ^ { 3 } + 5 x ^ { 2 } - 7 x + 1 \right)$

Use the grid to graph the function. Find the limit, if it exists - $\lim _ { x \rightarrow 1 } f ( x ) , f ( x ) = | 5 x |$

Find the limit as x approaches c of the average rate of change of the function from c to x. -c = -4; $f ( x ) = x ^ { 3 }$

Approximate the area under the curve and above the x-axis using n rectangles. Let the height of each rectangle be given by the value of the function at the right side of the rectangle. - $f ( x ) = 2 x ^ { 2 } + x + 3 \text { from } x = - 2 \text { to } x = 1 ; n = 6$

Find the equation of the tangent line to the graph of f at the given point. - $f ( x ) = x ^ { 2 } + 11 x - 15 \text { at } ( 1 , - 3 )$

Determine whether f is continuous at c. - $f ( x ) = \frac { - 1 } { x ^ { 2 } + 8 x } ; \quad c = - 8$

Find the limit algebraically. - $\lim _ { x \rightarrow 4 } \left( x ^ { 2 } + 4 x + 1 \right)$

Find the limit algebraically. - $\lim _ { x \rightarrow 0 } \frac { 3 \tan x } { 7 x }$

Approximate the area under the curve and above the x-axis using n rectangles. Let the height of each rectangle be given by the value of the function at the right side of the rectangle. - $f ( x ) = x ^ { 2 } + 2 \text { from } x = 1 \text { to } x = 4 ; n = 6$

Determine whether f is continuous at c. - $f ( x ) = \frac { 5 } { x ^ { 2 } - 2 x } ; \quad c = 0$

Use the TABLE feature of a graphing utility to find the limit. - $\lim _ { d \rightarrow } \left( \frac { d ^ { 3 } - 27 } { d - 3 } \right)$

Use the grid to graph the function. Find the limit, if it exists - $\lim _ { x \rightarrow 2 } f ( x ) , \quad f ( x ) = 4 x + 2$

Find the one-sided limit. - $\lim _ { x \rightarrow 3 } \frac { x ^ { 2 } - 2 x - 15 } { x + 3 }$