Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Use the graph of y = g(x) to answer the question. 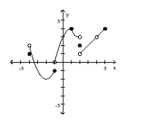 -What is the domain of g? A)
B) or
C)
D) or or
-What is the domain of g? A)
B) or
C)
D) or or
(Multiple Choice)
4.8/5  (31)
(31)
Use the TABLE feature of a graphing utility to find the limit.
-
(Multiple Choice)
4.8/5  (24)
(24)
Find the limit as x approaches c of the average rate of change of the function from c to x.
-c = 9;
(Multiple Choice)
4.7/5  (32)
(32)
Find the limit as x approaches c of the average rate of change of the function from c to x.
-c = 4; A)
B)
C)
D) Does not exist
(Multiple Choice)
4.7/5  (40)
(40)
Find the derivative of the function at the given value of x.
-
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-(a) What area does the integral represent?
(b) Use a graphing utility to approximate the area to three decimal places.
(Short Answer)
4.9/5  (28)
(28)
Solve the problem.
-A foul tip of a baseball is hit straight upward from a height of 4 feet with an initial velocity of 112 feet per second. The function 4 describes the ball's height above the ground, s(t), in feet, t seconds
After it was hit. The ball reaches its maximum height above the ground when the instantaneous speed reaches
Zero. After how many seconds does the ball reach its maximum height? A) 112
B)
C)
D) 7
(Multiple Choice)
4.8/5  (44)
(44)
Approximate the area under the curve and above the x-axis using n rectangles. Let the height of each rectangle be given
by the value of the function at the right side of the rectangle.
-
(Multiple Choice)
5.0/5  (28)
(28)
Find the numbers at which f is continuous. At which numbers is f discontinuous?
-
(Multiple Choice)
4.7/5  (36)
(36)
Solve the problem.
-Provide a graph that illustrates the area represented by the integral.
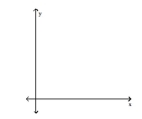 A)
A)
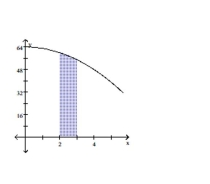 B)
B)
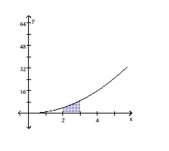 C)
C)
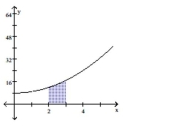 D)
D)
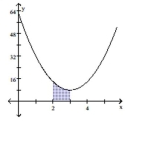
(Multiple Choice)
4.7/5  (35)
(35)
Showing 81 - 100 of 145
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)