Exam 10: Rational Exponents, Radicals, and Complex Numbers
Exam 1: Review of Real Numbers490 Questions
Exam 2: Equations, Inequalities, and Problem Solving332 Questions
Exam 3: Graphing313 Questions
Exam 4: Solving Systems of Linear Equations146 Questions
Exam 5: Exponents and Polynomials304 Questions
Exam 6: Factoring Polynomials261 Questions
Exam 7: Rational Expressions327 Questions
Exam 8: More on Functions and Graphs192 Questions
Exam 9: Inequalities and Absolute Value148 Questions
Exam 10: Rational Exponents, Radicals, and Complex Numbers379 Questions
Exam 11: Quadratic Equations and Functions242 Questions
Exam 12: Exponential and Logarithmic Functions302 Questions
Exam 13: Conic Sections153 Questions
Exam 14: Sequences, Series, and the Binomial Theorem201 Questions
Select questions type
Perform the indicated operation and simplify. Write the result in the form a
-
(Multiple Choice)
4.8/5  (42)
(42)
Simplify the radical expression. Assume that all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (39)
(39)
Multiply, and then simplify if possible. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (28)
(28)
Use the product rule to multiply. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.9/5  (44)
(44)
Multiply, and then simplify if possible. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (39)
(39)
Simplify. Assume that all variables represent any real number.
-
(Multiple Choice)
4.9/5  (31)
(31)
Find the root. Assume that all variables represent nonnegative real numbers.
-
(Multiple Choice)
4.9/5  (42)
(42)
Use the properties of exponents to simplify the expression. Write with positive exponents.
-
(Multiple Choice)
4.7/5  (41)
(41)
Rationalize the denominator and simplify. Assume that all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (39)
(39)
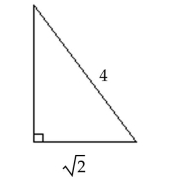
Use the Pythagorean theorem to find the unknown side of the right triangle.
-
(Multiple Choice)
4.7/5  (41)
(41)
Solve.
-The maximum number of volts, , that can be placed across a resistor is given by the formula , where is the number of watts of power that the resistor can absorb and is the resistance of the resistor in ohms. If a 2-watt resistor can have at most 20 volts of electricity across it, find the number of ohms of resistance of this resistor.
(Multiple Choice)
4.9/5  (45)
(45)
Use the product rule to multiply. Assume all variables represent positive real numbers.
-
(Multiple Choice)
5.0/5  (34)
(34)
Solve.
-The maximum number of volts, E, that can be placed across a resistor is given by the formula , where is the number of watts of power that the resistor can absorb and is the resistance of the resistor in ohms. If a -watt resistor has a resistance of 10,000 ohms, find the largest number of volts of electricity that could be placed across the resistor.
(Multiple Choice)
4.7/5  (33)
(33)
Rationalize the denominator and simplify. Assume that all variables represent positive real numbers.
-
(Multiple Choice)
4.9/5  (45)
(45)
Showing 201 - 220 of 379
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)