Exam 10: Rational Exponents, Radicals, and Complex Numbers
Exam 1: Review of Real Numbers490 Questions
Exam 2: Equations, Inequalities, and Problem Solving332 Questions
Exam 3: Graphing313 Questions
Exam 4: Solving Systems of Linear Equations146 Questions
Exam 5: Exponents and Polynomials304 Questions
Exam 6: Factoring Polynomials261 Questions
Exam 7: Rational Expressions327 Questions
Exam 8: More on Functions and Graphs192 Questions
Exam 9: Inequalities and Absolute Value148 Questions
Exam 10: Rational Exponents, Radicals, and Complex Numbers379 Questions
Exam 11: Quadratic Equations and Functions242 Questions
Exam 12: Exponential and Logarithmic Functions302 Questions
Exam 13: Conic Sections153 Questions
Exam 14: Sequences, Series, and the Binomial Theorem201 Questions
Select questions type
Rationalize the denominator and simplify. Assume that all variables represent positive real numbers.
-
(Multiple Choice)
4.9/5  (48)
(48)
Simplify the radical expression. Assume that all variables represent positive real numbers.
-
(Multiple Choice)
4.9/5  (38)
(38)
Find the square root. Assume that all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-The maximum distance in kilometers that you can see from a height in meters is given by the formula . How high above the ground must you be to see 35 kilometers. (Round to the nearest tenth of a meter.)
(Multiple Choice)
4.8/5  (39)
(39)
Multiply, and then simplify if possible. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.9/5  (34)
(34)
Fill in the blank with one of the words or phrases listed below. index rationalizing conjugate principal square rootcube root midpoint complex numberlike radicals radicand imaginary unit distance
-In the natation 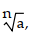 n is called the and a is called the ---------------
n is called the and a is called the ---------------
(Multiple Choice)
4.8/5  (40)
(40)
Use the product rule to multiply. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.9/5  (40)
(40)
Add or subtract. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.7/5  (33)
(33)
Find the midpoint of the line segment whose endpoints are given.
-
(Multiple Choice)
4.7/5  (39)
(39)
Solve.
-Find the area of the trapezoid. Simplify if possible.
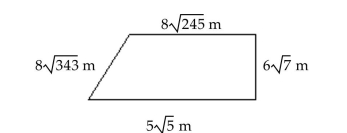
(Multiple Choice)
4.8/5  (38)
(38)
Simplify the radical expression. Assume that all variables represent positive real numbers.
-
(Multiple Choice)
4.9/5  (40)
(40)
Use the product rule to multiply. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (28)
(28)
Showing 261 - 280 of 379
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)