Exam 3: Exponential and Logarithmic Functions
Exam 1: Functions and Their Graphs120 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions120 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability118 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus120 Questions
Select questions type
Find the exponential model that fits the points shown in the table below. Round parameters to the nearest thousandth.
x 0 1 y 5 10
(Multiple Choice)
4.9/5  (39)
(39)
Condense the expression below to the logarithm of a single quantity.
(Multiple Choice)
4.9/5  (33)
(33)
Solve the logarithmic equation below algebraically. Round your result to three decimal places.
(Multiple Choice)
4.9/5  (25)
(25)
Solve the equation below algebraically. Round your result to three decimal places.
(Multiple Choice)
4.8/5  (30)
(30)
The sales (in thousands of units) of a cleaning solution after hundred dollars is spent on advertising are given by . When is spent on advertising, 2500 units are sold. Complete the model by solving for and use the model to estimate the number of units that will be sold if advertising
expenditures are raised to . Round your answer to the nearest unit.
(Multiple Choice)
4.7/5  (23)
(23)
Find the exponential model that fits the points shown in the graph when and . Round parameters to the nearest thousandth.
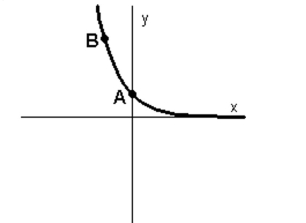
(Multiple Choice)
4.9/5  (36)
(36)
Use the properties of logarithms to expand the expression as a sum, difference, and/or constant multiple of logarithms. (Assume all variables are positive.)
(Multiple Choice)
4.7/5  (38)
(38)
D Determine which -value below is a solution of the equation .
(Multiple Choice)
4.8/5  (37)
(37)
Solve the exponential equation below algebraically. Round your result to three decimal places.
(Multiple Choice)
4.8/5  (31)
(31)
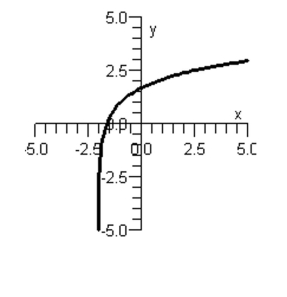
Match the function with its graph.
Graph I:
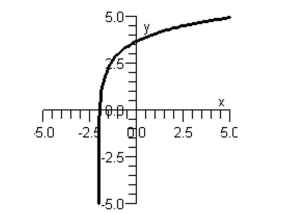 Graph II:
Graph II:
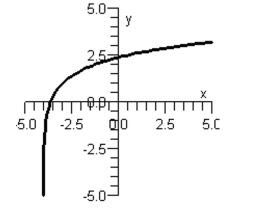 Graph III:
Graph III:
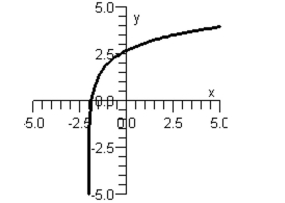 Graph IV:
Graph IV:
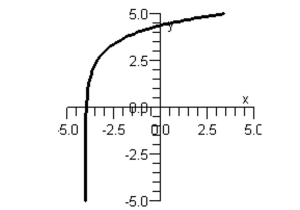 Graph V:
Graph V:
(Multiple Choice)
4.9/5  (31)
(31)
Condense the expression below to the logarithm of a single quantity.
(Multiple Choice)
4.8/5  (41)
(41)
Find the exact value of the logarithm without using a calculator, if possible.
(Multiple Choice)
4.9/5  (40)
(40)
Use the properties of logarithms to expand the expression as a sum, difference, and/or constant multiple of logarithms. (Assume all variables are positive.)
(Multiple Choice)
4.8/5  (28)
(28)
Showing 61 - 80 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)