Exam 10: Analytic Geometry in Three Dimensions
Exam 1: Functions and Their Graphs120 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions120 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability118 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus120 Questions
Select questions type
Find a set of parametric equations for the line through the point and parallel to the specified line. Show all your work.
, parallel to
y=3-4t z=-2+6t
Free
(Essay)
4.8/5  (31)
(31)
Correct Answer:
Answers may vary. One possible answer is shown below.
The lights in an auditorium are 25-pound disks of radius 16 inches. Each disk is supported by three equally spaced 50 -inch wires attached to the ceiling. Find the tension in each wire. Round your answer to two decimals.
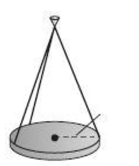
Free
(Multiple Choice)
4.7/5  (34)
(34)
Correct Answer:
C
The lights in an auditorium are 30-pound disks of radius 24 inches. Each disk is supported by three equally spaced 45 -inch wires attached to the ceiling. Find the tension in each wire. Round your answer to two decimals.
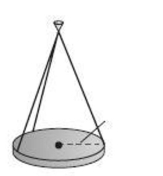
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
C
Find the angle of intersection of the planes in degrees. Round to a tenth of a degree.
3x-2y+5z=3 -x+3y+3z=3
(Multiple Choice)
4.8/5  (32)
(32)
Find the distance between the point and the plane.
(-2,-1,-4) -3x-2y-z=1
(Multiple Choice)
4.7/5  (43)
(43)
Find the area of the parallelogram that has the vectors as adjacent sides.
(Multiple Choice)
4.8/5  (32)
(32)
Find the general form of the equation of the plane passing through the point and perpendicular to the specified line.
(Multiple Choice)
4.8/5  (37)
(37)
The weight of a crate is 300 newtons. Find the tension in each of the supporting cables shown in the figure. The coordinates of the points , and are given below the figure. Round to the nearest newton.
![The weight of a crate is 300 newtons. Find the tension in each of the supporting cables shown in the figure. The coordinates of the points A , B , C , and D are given below the figure. Round to the nearest newton. [Figure not necessarily to scale.] point A = ( 0,0 , - 130 ) , point B = ( 90,0,0 ) , point C = ( - 40,40,0 ) , point D = ( 0 , - 1](https://storage.examlex.com/TB7699/11ecdb2e_9e9e_3668_a7e5_e587aea397f7_TB7699_11.jpg) [Figure not necessarily to scale.]
point , point , point , point
[Figure not necessarily to scale.]
point , point , point , point
(Multiple Choice)
4.8/5  (34)
(34)
Find the area of the parallelogram formed by the points , , and .
(Multiple Choice)
4.8/5  (34)
(34)
Find the angle, in degrees, between two adjacent sides of the pyramid shown below. Round to the nearest tenth of a degree. [Note: The base of the pyramid is not considered a side.]
![Find the angle, in degrees, between two adjacent sides of the pyramid shown below. Round to the nearest tenth of a degree. [Note: The base of the pyramid is not considered a side.]](https://storage.examlex.com/TB7699/11ecdb2f_1cde_4fbf_a7e5_c70d126be604_TB7699_11.jpg)
(Multiple Choice)
4.9/5  (39)
(39)
Find the angle between the vectors and . Express your answer in degrees and round to the nearest tenth of a degree.
(Multiple Choice)
4.8/5  (36)
(36)
Find the volume of the parallelpiped with the given vertices.
(Multiple Choice)
4.7/5  (41)
(41)
Find the lengths of the sides of the right triangle whose vertices are located at the given points. Show that these lengths satisfy the Pythagorean Theorem. Show all of your work.
(Essay)
4.8/5  (30)
(30)
Find the area of the parallelogram that has the vectors as adjacent sides.
(Multiple Choice)
4.9/5  (27)
(27)
Showing 1 - 20 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)