Exam 11: Limits and an Introduction to Calculus
Exam 1: Functions and Their Graphs120 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions120 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability118 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus120 Questions
Select questions type
Approximate the area of the region under the function below on the interval using 8 rectangles. Round your answer to two decimals.
Free
(Multiple Choice)
4.7/5  (36)
(36)
Correct Answer:
B
Estimate the following limit numerically, if it exists.
Free
(Multiple Choice)
4.7/5  (35)
(35)
Correct Answer:
A
A union contract guarantees a salary increase yearly for 3 years. For a current salary of , the salary (in thousands of dollars) for the next 3 years is given by
where represents the time in years. Find the limit of as , if it exists.
(Multiple Choice)
4.8/5  (42)
(42)
Use the first six terms to predict the limit of the sequence (assume begins with 1).
(Multiple Choice)
4.7/5  (22)
(22)
Approximate the area of the indicated region under the given curve using five rectangles.
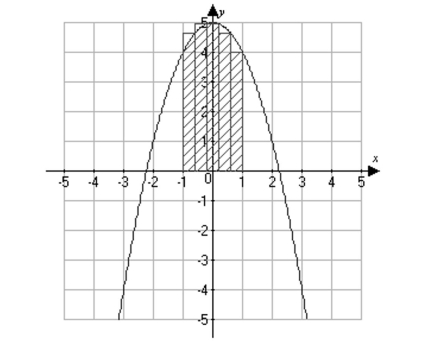
(Multiple Choice)
4.8/5  (35)
(35)
Consider the following graph of the function and approximate , if it exists.
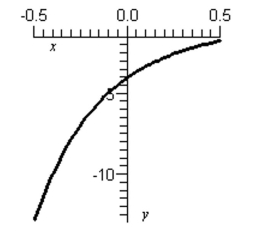
(Multiple Choice)
4.9/5  (35)
(35)
Find the following limit. Round your answer to two decimals.
(Multiple Choice)
4.8/5  (38)
(38)
Use the figure below to approximate the slope of the curve at the point .
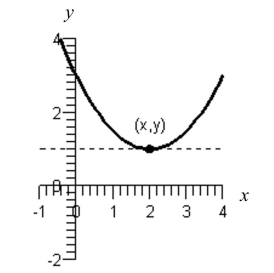
(Multiple Choice)
4.8/5  (30)
(30)
Using the summation formulas and properties, evaluate the following expression.
(Multiple Choice)
4.8/5  (40)
(40)
A union contract guarantees a salary increase yearly for 3 years. For a current salary of , the salary (in thousands of dollars) for the next 3 years is given by
where represents the time in years. Find the limit of as , if it exists.
(Multiple Choice)
4.7/5  (38)
(38)
Showing 1 - 20 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)