Exam 7: Linear Systems and Matrices
Exam 1: Functions and Their Graphs120 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions120 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability118 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus120 Questions
Select questions type
Find the minor and its cofactor of the matrix .
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
E
Find the equation of the parabola that passes through the points.
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
E
Determine whether the two systems of linear equations yield the same solutions. If so, find the solutions using matrices.
x+9y+9z =-22 y-6z =-23 z =3 x+8y-5z =-63 y+4z =7 z =3
(Multiple Choice)
4.9/5  (29)
(29)
Determine whether the two systems of linear equations yield the same solutions. If so, find the solutions using matrices.
x+9y-2z =41 y-7z =46 z =-6 x+4y+2z =-3 y+5z =-26 z =-6
(Multiple Choice)
4.8/5  (44)
(44)
Use a system of equations to find the specified equation that passes through the points. Solve the system using matrices.
Parabola:
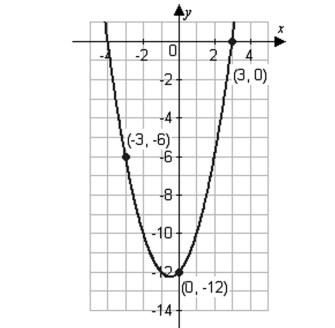
(Multiple Choice)
4.9/5  (33)
(33)
Write the system of linear equations as a matrix equation , and use GaussJordan elimination on the augmented matrix to solve for the matrix .
(Multiple Choice)
4.9/5  (37)
(37)
Solve the system of linear equations
using the inverse matrix .
(Multiple Choice)
4.8/5  (44)
(44)
Find the equation of the circle
that passes through the points .
(Multiple Choice)
4.8/5  (27)
(27)
Solve for given the following equation involving a determinant.
(Multiple Choice)
4.8/5  (31)
(31)
Write the system of linear equations represented by the augmented matrix. Then use back-substitution to solve. (Use variables , and .)
(Multiple Choice)
4.8/5  (37)
(37)
Determine whether the system of linear equations is consistent or inconsistent.
(Multiple Choice)
4.9/5  (35)
(35)
An object moving vertically is at the given heights at the specified times. Find the position equation for the object.
At second, feet
At seconds, feet
At seconds, feet
(Multiple Choice)
4.8/5  (36)
(36)
Determine which one of the ordered triples below is a solution of the given system of equations.
(Multiple Choice)
4.8/5  (35)
(35)
Showing 1 - 20 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)