Exam 7: Linear Systems and Matrices
Exam 1: Functions and Their Graphs120 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions120 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability118 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus120 Questions
Select questions type
Use a system of equations to find the specified equation that passes through the points. Solve the system using matrices.
Parabola:
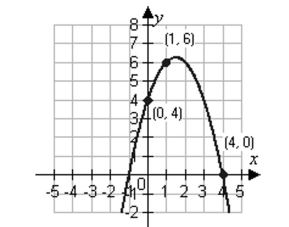
(Multiple Choice)
4.8/5  (28)
(28)
Perform the indicated row operations on the matrix. Show the final result.
Add times to .
Add times to .
(Multiple Choice)
4.8/5  (37)
(37)
Solve the system of linear equations
using the inverse matrix .
(Multiple Choice)
4.8/5  (38)
(38)
Solve the system of linear equations
using the inverse matrix
(Multiple Choice)
4.8/5  (31)
(31)
Use a determinant to determine whether the points below are collinear.
(Multiple Choice)
4.8/5  (19)
(19)
Find the determinant of by the method of expansion by cofactors.
(Multiple Choice)
4.7/5  (42)
(42)
Use the matrix capabilities of a graphing utility to reduce the augmented matrix corresponding to the system of equations, and solve the system.
(Multiple Choice)
4.9/5  (35)
(35)
Use the matrix capabilities of a graphing utility to find , if possible.
(Multiple Choice)
4.9/5  (31)
(31)
Find the equilibrium point of the demand and supply equations. (The equilibrium point is the price and number of units that satisfy both the demand and supply equations.)
Demand Supply p=130-0.09x p=0.4x-115
(Multiple Choice)
4.8/5  (36)
(36)
Showing 101 - 120 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)