Exam 12: Regular Expressions and Finite State Automata
Prove that there is no finite-state automaton that accepts the language consisting of all strings of 's and 's of the form where is a positive integer.
![Suppose not. That is suppose there is a finite-state automaton A that accepts the language L consisting of all strings of x 's and y 's of the form x^{n} y^{n} where n is a positive integer. [A contradiction will be derived.] Since A has only a finite number of states, these states can be denoted s_{1}, s_{2}, s_{3}, \ldots, s_{k} , where k is a positive integer.Consider all input strings that consist entirely of x 's: x, x^{2}, x^{3}, \ldots . Now there are infinitely many such strings and only finitely many states. Thus, by the pigeonhole principle, there must be a state s_{m} and two input strings x^{p} and x^{q} with p \neq q such that when either x^{p} or x^{q} are input to A, A goes to state s_{m} . Now, by supposition, A accepts the string x^{p} y^{p} . This means that after p x^{\prime} 's have been input, at which point A is in state s_{m} , inputting p additional b's sends A into an accepting state, say s_{a} . But that implies that inputting x^{q} y^{p} also sends A to s_{a} , which means that x^{q} y^{p} is also accepted by A . The reason is that after q x 's have been input, A is also in state s_{m} , and from that point, we know that inputting p additional b's sends A to state s_{a} , which is an accepting state. Hence x ^ { q } y ^ { p } is in L where p \neq q But, by supposition, all the strings in L have the form x ^ { n } y ^ { n } , which have the same number of that there is no finite-state automaton that accepts the language L consisting of all strings of x ^ { \prime } 's and y 's of the form x ^ { n } y ^ { n } where n is a positive integer.](https://storage.examlex.com/TB7212/11eccf81_5bb5_1f32_bf92_0d2de0da79b9_TB7212_11.jpg) Suppose not. That is suppose there is a finite-state automaton that accepts the language consisting of all strings of 's and 's of the form where is a positive integer. [A contradiction will be derived.] Since has only a finite number of states, these states can be denoted , where is a positive integer.Consider all input strings that consist entirely of 's: . Now there are infinitely many such strings and only finitely many states. Thus, by the pigeonhole principle, there must be a state and two input strings and with such that when either or are input to goes to state . Now, by supposition, accepts the string . This means that after 's have been input, at which point is in state , inputting additional b's sends into an accepting state, say . But that implies that inputting also sends to , which means that is also accepted by . The reason is that after 's have been input, is also in state , and from that point, we know that inputting additional b's sends to state , which is an accepting state. Hence
Suppose not. That is suppose there is a finite-state automaton that accepts the language consisting of all strings of 's and 's of the form where is a positive integer. [A contradiction will be derived.] Since has only a finite number of states, these states can be denoted , where is a positive integer.Consider all input strings that consist entirely of 's: . Now there are infinitely many such strings and only finitely many states. Thus, by the pigeonhole principle, there must be a state and two input strings and with such that when either or are input to goes to state . Now, by supposition, accepts the string . This means that after 's have been input, at which point is in state , inputting additional b's sends into an accepting state, say . But that implies that inputting also sends to , which means that is also accepted by . The reason is that after 's have been input, is also in state , and from that point, we know that inputting additional b's sends to state , which is an accepting state. Hence
is in where
But, by supposition, all the strings in have the form , which have the same number of that there is no finite-state automaton that accepts the language consisting of all strings of 's and 's of the form where is a positive integer.
Consider the regular expression
(a) Describe the language defined by this expression.
(b) Design a finite-state automaton to accept the language defined by the expression.
a. The language accepted by the automaton is the set of all strings of 0 's and 1 's that contain exactly one 1 or that contain exactly two 1 's.
b.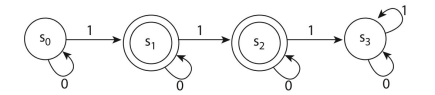
Consider the finite-state automaton given by the following transition diagram: 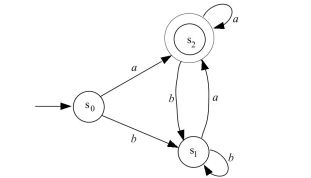 (a) What is ?
(b) To what state does the automaton go if the string babaa is input to it?
(c) Indicate which of the following strings are accepted by the automaton:
(d) Describe the language accepted by this automaton.
(e) Find a regular expression that defines the same language.
(a) What is ?
(b) To what state does the automaton go if the string babaa is input to it?
(c) Indicate which of the following strings are accepted by the automaton:
(d) Describe the language accepted by this automaton.
(e) Find a regular expression that defines the same language.
a.
b.
c. The strings and are accepted by the automaton. The strings and are not accepted by the automaton.
d. The language accepted by the automaton is the set of all strings of 's and 's that end in an .
e.
Consider the finite-state automaton given by the following transition diagram: 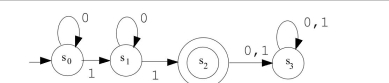 (a) To what state does the automaton go if the string 10010010 is input to it? Is this string accepted by the automaton?
(b) Indicate which of the following strings are accepted by the automaton: 000101 0100010 000100 110001
(c) Describe the language accepted by the automaton.
(d) Find a regular expression that defines the same language.
(a) To what state does the automaton go if the string 10010010 is input to it? Is this string accepted by the automaton?
(b) Indicate which of the following strings are accepted by the automaton: 000101 0100010 000100 110001
(c) Describe the language accepted by the automaton.
(d) Find a regular expression that defines the same language.
Let , and let be the language over consisting of all strings of 0 's and 1 's of length 4 with an equal number of 0 's and 1's. List the elements of .
Let be the language defined by the regular expression .
(a) Write 3 strings that belong to
(b) Use words to describe .
Consider the finite-state automaton given by the following next-state table:  (a) Draw the transition diagram for this automaton.
(b) Indicate which of the following strings are accepted by the automaton: 0100 1001 0110 101010
(c) Describe the language accepted by the automaton.
(d) Find a regular expression that defines the same language.
(a) Draw the transition diagram for this automaton.
(b) Indicate which of the following strings are accepted by the automaton: 0100 1001 0110 101010
(c) Describe the language accepted by the automaton.
(d) Find a regular expression that defines the same language.
Consider the language that consists of all strings of 0 's and 1's in which the number of 1's is evenly divisible by 4 . Find a regular expression that defines this language.
Consider the regular expression
(a) Describe the language defined by this expression.
(b) Design a finite-state automaton to accept the language defined by the expression.
Let be the language defined by the regular expression .
(a) Write 3 strings that belong to
(b) Use words to describe .
Consider the finite-state automaton given by the following next-state table:  (a) Draw the transition diagram for the automaton.
(b) Indicate which of the following strings are accepted by the automaton: 0100 101 1110 00101
(c) Describe the language accepted by this automaton.
(d) Find a regular expression that defines the same language.
(a) Draw the transition diagram for the automaton.
(b) Indicate which of the following strings are accepted by the automaton: 0100 101 1110 00101
(c) Describe the language accepted by this automaton.
(d) Find a regular expression that defines the same language.
Consider the language that consists of all strings of 's and 's in which the second character from the beginning is a . Find a regular expression that defines this language.
Consider the finite-state automaton given by the following next-state table:  (a) Draw the transition diagram for this automaton.
(b) Indicate which of the following strings are accepted by the automaton:
(c) Describe the language accepted by the automaton.
(d) Find a regular expression that defines the same language.
(a) Draw the transition diagram for this automaton.
(b) Indicate which of the following strings are accepted by the automaton:
(c) Describe the language accepted by the automaton.
(d) Find a regular expression that defines the same language.
Finite-state automata and are defined by the transition diagrams shown below.
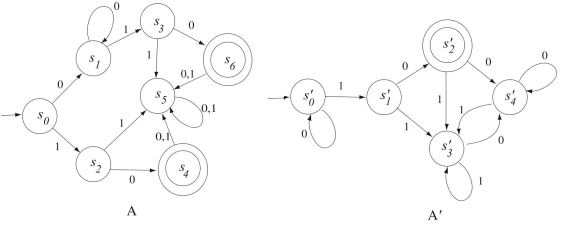 (a) Find the quotient automaton for A.
(b) Find the quotient automaton for
(c) Are A and equivalent? Explain.
(a) Find the quotient automaton for A.
(b) Find the quotient automaton for
(c) Are A and equivalent? Explain.
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)