Exam 12: Fractal Geometry: the Kinky Nature of Nature
Exam 1: The Mathematics of Elections: the Paradoxes of Democracy40 Questions
Exam 2: The Mathematics of Power: Weighted Voting40 Questions
Exam 3: The Mathematics of Sharing: Fair-Division Games38 Questions
Exam 4: The Mathematics of Apportionment: Making the Rounds40 Questions
Exam 5: The Mathematics of Getting Around: Euler Paths and Circuits37 Questions
Exam 6: The Mathematics of Touring: Traveling Salesman Problems40 Questions
Exam 7: The Cost of Being Connected40 Questions
Exam 8: The Mathematics of Scheduling: Chasing the Critical Path40 Questions
Exam 9: Population Growth Models: There Is Strength in Numbers40 Questions
Exam 10: Financial Mathematics: Money Matters40 Questions
Exam 11: The Mathematics of Symmetry: Beyond Reflection40 Questions
Exam 12: Fractal Geometry: the Kinky Nature of Nature39 Questions
Exam 13: Fibonacci Numbers and the Golden Ratio: Tales of Rabbits and Gnomons40 Questions
Exam 14: Censuses, Surveys, Polls, and Studies: the Joys of Collecting Data40 Questions
Exam 15: Graphs, Charts, and Numbers: the Data Show and Tell40 Questions
Exam 16: Probabilities, Odds, and Expectations: Measuring Uncertainty and Risk40 Questions
Exam 17: The Mathematics of Normality: the Call of the Bell40 Questions
Select questions type
The following is called the Chaos Game. Start with a square ABCD in which A is located at (0,0), B is located at (27,0), C is located at (27,27) , and D is located at (0,27) . Then, roll a fair die. We will say that A is the winner if we roll a 1, B is the winner if we roll a 2, C is the winner if we roll a 3, and D is the winner if we roll a 4 . If we roll a 5 or 6 , we disregard the roll and roll again. Each roll of the die generates a point inside or on the boundary of the square according to the following rules.
- Start: Roll the die. Mark the winning vertex and call it P1.
- Step 1: Roll the die again. From P1 move two-thirds of the way straight towards the next winning vertex. Mark this point and call it P2 .
- Steps 2,3, etc.: Continue rolling the die, each time moving to a point two-thirds of the way from the last position to the winning vertex.
The grid below show the square ABCD .
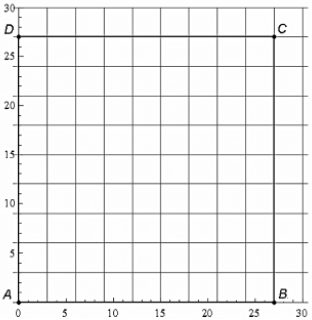 What would be the resulting coordinates of P3 if the sequence of (4,1,4) was rolled?
What would be the resulting coordinates of P3 if the sequence of (4,1,4) was rolled?
(Short Answer)
5.0/5  (44)
(44)
To answer the following question, refer to the Mandelbrot replacement process described by:
Start: Choose an arbitrary complex number s , called the seed of the Mandelbrot sequence. Set the seed s as the initial term of the sequence: 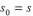 Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed:
Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed: 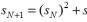 If the seed is
If the seed is  , then find the term
, then find the term 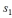
(Short Answer)
4.8/5  (31)
(31)
 -Refer to the information from table shown above ; what is the perimeter of the Koch snowflake created if the Step process were to continue indefinitely?
-Refer to the information from table shown above ; what is the perimeter of the Koch snowflake created if the Step process were to continue indefinitely?
(Multiple Choice)
4.9/5  (46)
(46)
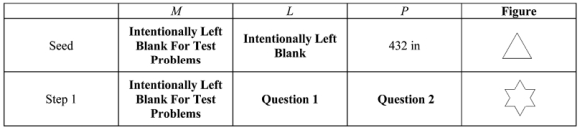
You plan on constructing a Sierpinski gasket by starting with a seed triangle whose area is 6720 in2. The table below gives the following information where R is the number of triangles removed at a
Particular step, S is the area of each removed triangle, and T is the total area of the newly created figure.
 What is the total area of the figure after step 2 ?
What is the total area of the figure after step 2 ?
(Multiple Choice)
4.9/5  (35)
(35)
 -Refer to the table shown above ; what is the total area of the figure after Step 3?
-Refer to the table shown above ; what is the total area of the figure after Step 3?
(Short Answer)
4.9/5  (38)
(38)
To answer the following question, refer to the Mandelbrot replacement process described by:
- Start: Choose an arbitrary complex number s , called the seed of the Mandelbrot sequence. Set the seed as the initial term of the sequence: 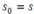 - Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed:
- Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed: 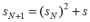 If the seed is
If the seed is 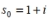 , then find the term
, then find the term 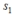 .
.
(Short Answer)
4.8/5  (38)
(38)
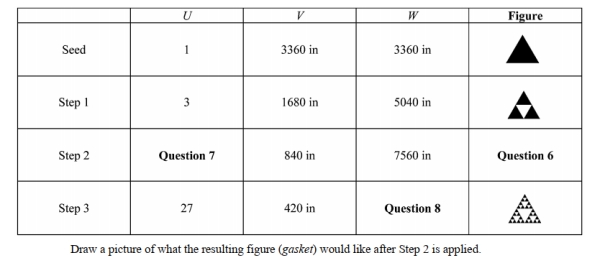 -Refer to the information from table shown above ; what is the total length of the darkened boundary of the Sierpinski gasket created if the Step process were to continue indefinitely?
-Refer to the information from table shown above ; what is the total length of the darkened boundary of the Sierpinski gasket created if the Step process were to continue indefinitely?
(Short Answer)
4.9/5  (31)
(31)
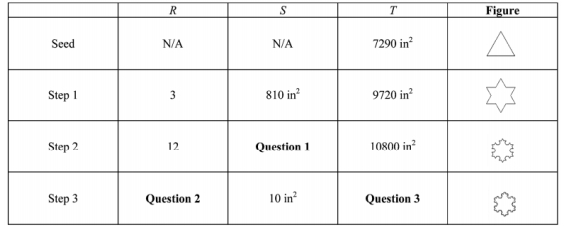 -Refer to the table shown above ; what is the total area of the figure after Step 3?
-Refer to the table shown above ; what is the total area of the figure after Step 3?
(Multiple Choice)
4.7/5  (32)
(32)
To answer the following question, refer to the Mandelbrot replacement process described by:
- Start: Choose an arbitrary complex number s, called the seed of the Mandelbrot sequence. Set the seed s to be the initial term of the sequence: 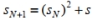 - Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed:
- Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed: 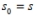 Which of the statements below is correct?
Which of the statements below is correct?
(Multiple Choice)
4.8/5  (36)
(36)
You plan on constructing a Koch snowflake by starting with a seed triangle whose perimeter is 432 in. The table below gives the following information where M is the number of sides at a particular step, L
Is the length of each side, and P is the total perimeter of the figure. What is the length of each side of the figure in Step 1?

(Multiple Choice)
4.9/5  (35)
(35)
The following is called the Chaos Game. Start with a square ABCD in which A is located at (0,0), B is located at (27,0), C is located at (27,27) , and D is located at (0,27) . Then, roll a fair die. We will say that A is the winner if we roll a 1, B is the winner if we roll a 2, C is the winner if we roll a 3 , and D is the winner if we roll a 4 . If we roll a 5 or 6 , we disregard the roll and roll again. Each roll of the die generates a point inside or on the boundary of the square according to the following rules.
- Start: Roll the die. Mark the winning vertex and call it P1 .
- Step 1: Roll the die again. From P1 move two-thirds of the way straight towards the next winning vertex. Mark this point and call it P2 .
- Steps 2,3, etc.: Continue rolling the die, each time moving to a point two-thirds of the way from the last position to the winning vertex.
The grid below show the square ABCD .
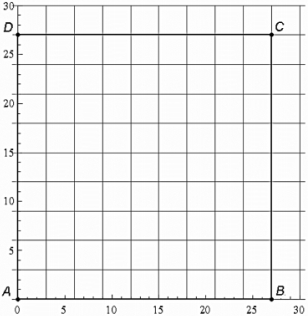 What would be the sequence (1,2,3) was rolled?
What would be the sequence (1,2,3) was rolled?
(Short Answer)
4.9/5  (35)
(35)
You plan on constructing a Sierpinski gasket by starting with a seed triangle whose perimeter is X. The table below gives the following information where U is the number of darkened triangles at a particular step, V is the perimeter of each darkened triangle, and W is the length of the darkened boundary of the figure (gasket) obtained in a particular step. 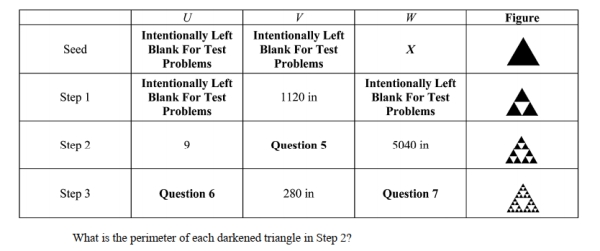
(Multiple Choice)
4.7/5  (45)
(45)
Which of the following is an example of fractal behavior in nature?
(Multiple Choice)
4.9/5  (30)
(30)
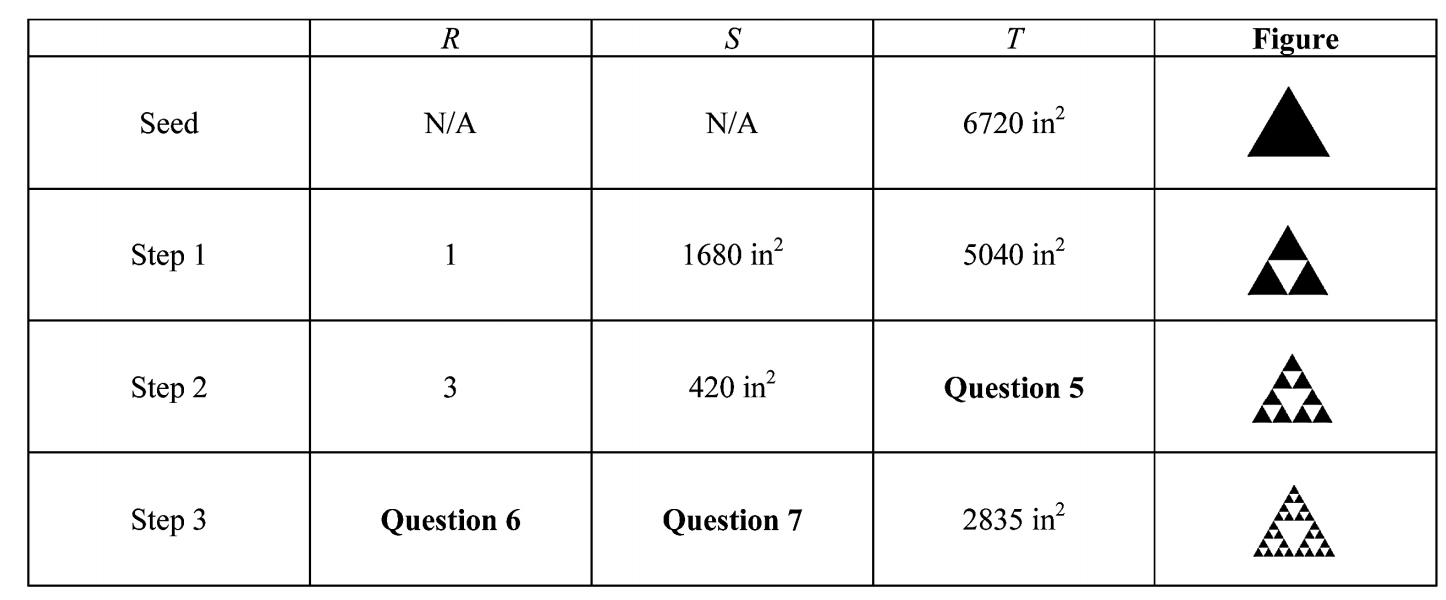
 -Refer to the information in the table shown above ; how many darkened triangles are there in Step 3?
-Refer to the information in the table shown above ; how many darkened triangles are there in Step 3?
(Multiple Choice)
4.9/5  (35)
(35)
 -Refer to the information in the table above ; what is the area of the Koch snowflake created if the Step
process were to continue indefinitely?
-Refer to the information in the table above ; what is the area of the Koch snowflake created if the Step
process were to continue indefinitely?
(Short Answer)
4.9/5  (37)
(37)
 -Refer to the table shown above ; what is the total perimeter length in Step 1?
(a) 324 in
(b) 576 in
(c) 648 in
(d) 1296 in
(e) None of the above.
-Refer to the table shown above ; what is the total perimeter length in Step 1?
(a) 324 in
(b) 576 in
(c) 648 in
(d) 1296 in
(e) None of the above.
(Short Answer)
4.8/5  (42)
(42)
 -Refer to the table shown above ; what is the area of each of the triangles removed during Step 3 ?
-Refer to the table shown above ; what is the area of each of the triangles removed during Step 3 ?
(Multiple Choice)
4.8/5  (41)
(41)
To answer the following question, refer to the Mandelbrot replacement process described by:
a. Start: Choose an arbitrary complex number s , called the seed of the Mandelbrot sequence. Set the seed s as the initial term of the sequence: 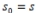 b. Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed:
b. Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed: 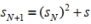 Which of the statements below is correct?
Which of the statements below is correct?
(Multiple Choice)
4.8/5  (37)
(37)
You plan on constructing a Koch snowflake by starting with a seed triangle whose perimeter is X. The table below gives the following information where M is the number of sides at a particular step, L is the length of each side, and P is the total perimeter of the figure. 
(Short Answer)
4.9/5  (36)
(36)
Showing 21 - 39 of 39
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)