Exam 4: Exponential and Logarithmic Functions
Exam 1: Equations and Inequalities420 Questions
Exam 2: Functions and Graphs83 Questions
Exam 3: Polynomial and Rational Functions98 Questions
Exam 4: Exponential and Logarithmic Functions268 Questions
Exam 5: Systems of Equations and Inequalities287 Questions
Exam 6: Matrices and Determinants152 Questions
Exam 7: Conic Sections120 Questions
Exam 8: Sequences, Induction, and Probability303 Questions
Select questions type
Use Natural Logarithms
Evaluate or simplify the expression without using a calculator.
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-A city is growing at the rate of 0.3% annually. If there were 2,520,000 residents in the city in 1993, find how many (to the nearest ten-thousand)are living in that city in 2000. Use y = 2,520,000(2.7)0.003t.
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-The function models the amount in pounds of a particular radioactive material stored in a concrete vault, where is the number of years since the material was put into the vault. Find the amount of radioactive material in the vault after 120 years. Round to the nearest whole number.
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Cindy will require $18,000 in 2 years to return to college to get an MBA degree. How much money should she ask her parents for now so that, if she invests it at 11% compounded continuously, she will have
Enough for school? (Round your answer to the nearest dollar.)
(Multiple Choice)
4.9/5  (35)
(35)
Use properties of logarithms to condense the logarithmic expression. Write the expression as a single logarithm
whose coefficient is 1. Where possible, evaluate logarithmic expressions.
-
(Multiple Choice)
4.9/5  (38)
(38)
Use Natural Logarithms
Evaluate or simplify the expression without using a calculator.
-
(Multiple Choice)
4.9/5  (31)
(31)
Use the Product Rule
Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate
logarithmic expressions without using a calculator.
-
(Multiple Choice)
4.8/5  (32)
(32)
Use properties of logarithms to condense the logarithmic expression. Write the expression as a single logarithm
whose coefficient is 1. Where possible, evaluate logarithmic expressions.
-
(Multiple Choice)
4.8/5  (36)
(36)
Use the Definition of a Logarithm to Solve Logarithmic Equations
Solve the logarithmic equation. Be sure to reject any value that is not in the domain of the original logarithmic
expressions. Give the exact answer.
-
(Multiple Choice)
4.9/5  (35)
(35)
Solve the exponential equation. Use a calculator to obtain a decimal approximation, correct to two decimal places,
for the solution.
-
(Multiple Choice)
4.9/5  (29)
(29)
Model Exponential Growth and Decay
Solve.
-The value of a particular investment follows a pattern of exponential growth. In the year 2000 , you invested money in a money market account. The value of your investment t years after 2000 is given by the exponential growth model . How much did you initially invest in the account?
(Multiple Choice)
4.9/5  (41)
(41)
Evaluate or simplify the expression without using a calculator.
-
(Multiple Choice)
4.7/5  (25)
(25)
Use Compound Interest Formulas
Use the compound interest formulas A
-Find the accumulated value of an investment of $2000 at 10% compounded semiannually for 7 years.
(Multiple Choice)
4.7/5  (26)
(26)
Model Exponential Growth and Decay
Solve.
-The half-life of silicon-32 is 710 years. If 30 grams is present now, how much will be present in 300 years? (Round your answer to three decimal places.)
(Multiple Choice)
4.7/5  (27)
(27)
Use the One-to-One Property of Logarithms to Solve Logarithmic Equations
Solve the logarithmic equation. Be sure to reject any value that is not in the domain of the original logarithmic
expressions. Give the exact answer.
-
(Multiple Choice)
4.7/5  (40)
(40)
Use properties of logarithms to condense the logarithmic expression. Write the expression as a single logarithm
whose coefficient is 1. Where possible, evaluate logarithmic expressions.
-
(Multiple Choice)
4.7/5  (41)
(41)
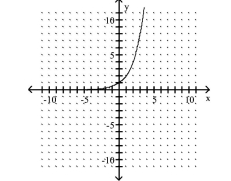
The graph of an exponential function is given. Select the function for the graph from the functions listed.
-
(Multiple Choice)
4.9/5  (26)
(26)
Showing 161 - 180 of 268
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)