Exam 12: Geometry Problems: Complementary Angles, Collinear Points, and Similar Triangles
Exam 1: Line and Angle Relationships13 Questions
Exam 2: Parallel Lines13 Questions
Exam 3: Triangles16 Questions
Exam 4: Quadrilaterals14 Questions
Exam 5: Similar Triangles12 Questions
Exam 6: Circles10 Questions
Exam 7: Locus and Concurrence4 Questions
Exam 8: Areas of Polygons and Circles5 Questions
Exam 9: Surfaces and Solids4 Questions
Exam 10: Analytical Geometry8 Questions
Exam 11: Introduction to Trigonometry4 Questions
Exam 12: Geometry Problems: Complementary Angles, Collinear Points, and Similar Triangles916 Questions
Select questions type
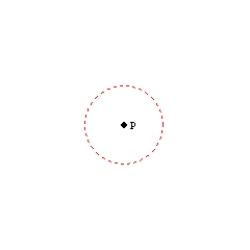 -The locus of points in space that are at a distance of 1 inch from point P is the circle with center P and a radius length of 1 inch.
-The locus of points in space that are at a distance of 1 inch from point P is the circle with center P and a radius length of 1 inch.
(True/False)
4.7/5  (39)
(39)
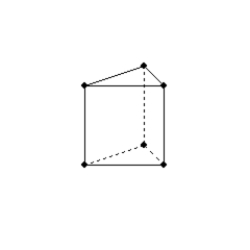 -What is the total number of faces for a prism whose base is a decagon?
-What is the total number of faces for a prism whose base is a decagon?
(Short Answer)
4.8/5  (24)
(24)
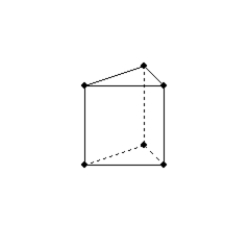 -Where B is the area of the base and h is the length of altitude, the volume of a prism and cylinder can both be found by the formula V = Bh.
-Where B is the area of the base and h is the length of altitude, the volume of a prism and cylinder can both be found by the formula V = Bh.
(True/False)
4.8/5  (28)
(28)
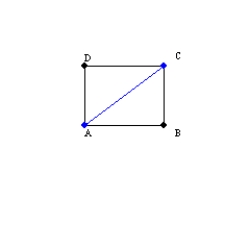 -For a quadrilateral to be a rectangle, how must the diagonals be related?
-For a quadrilateral to be a rectangle, how must the diagonals be related?
(Multiple Choice)
4.8/5  (25)
(25)
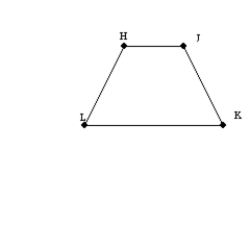 -If M and N are the midpoints of nonparallel sides
-If M and N are the midpoints of nonparallel sides 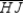 and
and 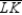 of trapezoid HJKL, then
of trapezoid HJKL, then 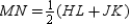 .
.
(True/False)
4.9/5  (34)
(34)
To construct the midpoint of the horizontal line segment 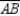 , begin by marking off arcs of equal length from points A and B so that the arcs intersect both above and below
, begin by marking off arcs of equal length from points A and B so that the arcs intersect both above and below 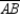 .
.
(True/False)
4.7/5  (33)
(33)
When two secants intersect at a point in the exterior of a circle, the measure of the angle formed is one-half the positive difference of the measures of the two intercepted arcs.
(True/False)
4.7/5  (32)
(32)
Given that 1 foot = 12 inches, what is the number of square inches in 1 square foot?
(Essay)
4.8/5  (33)
(33)
For a regular pentagon, find the measure of each central angle.
(Short Answer)
4.9/5  (37)
(37)
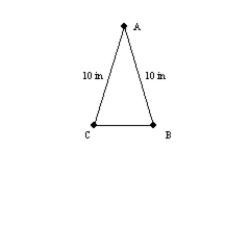 -In the isosceles triangle shown, the legs are 10 inches each while m
-In the isosceles triangle shown, the legs are 10 inches each while m  = 40°. Find the length of base
= 40°. Find the length of base 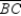 correct to the nearest tenth of an inch.
correct to the nearest tenth of an inch.
(Short Answer)
4.8/5  (29)
(29)
For what type of regular polygon does the apothem have a length equal to one-half the length of a side of the polygon?
(Short Answer)
4.8/5  (29)
(29)
In the form 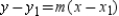 , find the equation of the line that is the perpendicular- bisector of the line segment that joins (0,0) and (2a,2b).
, find the equation of the line that is the perpendicular- bisector of the line segment that joins (0,0) and (2a,2b).
(Multiple Choice)
4.8/5  (43)
(43)
 -The locus of points in a plane that are equidistant from the sides of
-The locus of points in a plane that are equidistant from the sides of  is the bisector of
is the bisector of  .
.
(True/False)
4.7/5  (31)
(31)
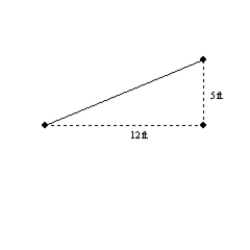 -In a right triangle, the measures of the angles are
-In a right triangle, the measures of the angles are  ,
, 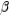 , and
, and 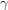 = 90°. With the lengths of the opposite sides being a, b, and c respectively, find tan
= 90°. With the lengths of the opposite sides being a, b, and c respectively, find tan 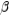 .
.
(Essay)
4.8/5  (34)
(34)
Find the length of base in an isosceles triangle with perimeter 25 inches and length of leg
8 inches.
(Short Answer)
4.8/5  (31)
(31)
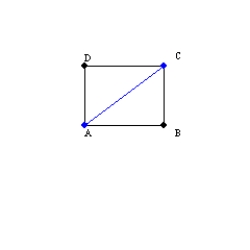 -When the midpoints of the sides of a square RSTV are joined in order, quadrilateral MNPQ is formed. Being as specific as possible, what type of quadrilateral is MNPQ?
-When the midpoints of the sides of a square RSTV are joined in order, quadrilateral MNPQ is formed. Being as specific as possible, what type of quadrilateral is MNPQ?
(Short Answer)
4.9/5  (37)
(37)
Showing 441 - 460 of 916
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)