Exam 12: Geometry Problems: Complementary Angles, Collinear Points, and Similar Triangles
Exam 1: Line and Angle Relationships13 Questions
Exam 2: Parallel Lines13 Questions
Exam 3: Triangles16 Questions
Exam 4: Quadrilaterals14 Questions
Exam 5: Similar Triangles12 Questions
Exam 6: Circles10 Questions
Exam 7: Locus and Concurrence4 Questions
Exam 8: Areas of Polygons and Circles5 Questions
Exam 9: Surfaces and Solids4 Questions
Exam 10: Analytical Geometry8 Questions
Exam 11: Introduction to Trigonometry4 Questions
Exam 12: Geometry Problems: Complementary Angles, Collinear Points, and Similar Triangles916 Questions
Select questions type
Where 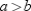 , the distance between the points (a, c) and (b, c) is (
, the distance between the points (a, c) and (b, c) is (  ) units.
) units.
(True/False)
4.8/5  (31)
(31)
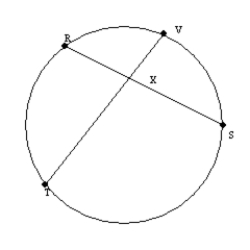 -For the circle shown, chords
-For the circle shown, chords  and
and 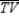 intersect at point X. With RX = 6, XS = 8, TX = x + 8 and XV = x, find the length of
intersect at point X. With RX = 6, XS = 8, TX = x + 8 and XV = x, find the length of 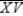 .
.
(Short Answer)
4.9/5  (33)
(33)
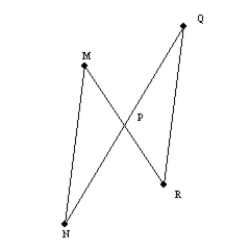 -
-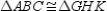 . In
. In 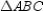 ,
, 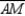 is the median from vertex A to side
is the median from vertex A to side 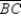 . Likewise,
. Likewise,  is the median of
is the median of 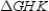 from vertex G to side
from vertex G to side 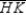 . How are
. How are 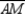 and
and  related?
related?
(Essay)
4.8/5  (41)
(41)
While the coordinate axes separate the Cartesian plane into 4 subsets (quadrants), the xy plane, xz plane, and yz plane separte Cartesian space into:
(Multiple Choice)
4.7/5  (40)
(40)
In 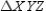 , the line segment
, the line segment 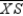 joins vertex
joins vertex 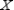 to point
to point 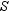 on the opposite side
on the opposite side 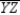 in such
a way that
in such
a way that 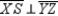 . In relation to
. In relation to 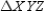 , what name is given to
, what name is given to 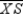 ?
?
(Short Answer)
4.8/5  (40)
(40)
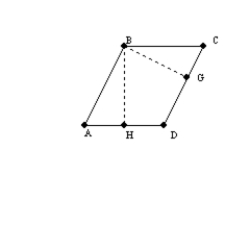 -The area of
-The area of  is 35.1
is 35.1  . Choosing a side of RSTV that measures 4.5 cm as the base, what is the length of the corresponding altitude?
. Choosing a side of RSTV that measures 4.5 cm as the base, what is the length of the corresponding altitude?
(Multiple Choice)
4.8/5  (36)
(36)
If the length of each apothem of a square is a, then the length of each side is 2a.
(True/False)
4.8/5  (35)
(35)
Given that 1 foot = 12 inches, how many cubic inches are in one cubic foot?
(Essay)
4.8/5  (40)
(40)
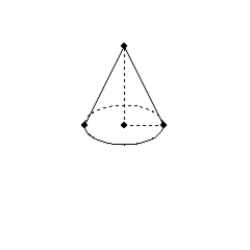 -A right circular cone has a radius of 6 inches and an altitude of 8 inches. Use
-A right circular cone has a radius of 6 inches and an altitude of 8 inches. Use 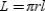 in order to find the exact total area of the cone.
in order to find the exact total area of the cone.
(Essay)
4.9/5  (28)
(28)
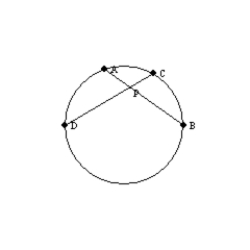 -In the circle, chords
-In the circle, chords 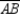 and
and 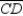 intersect at point P. If m
intersect at point P. If m 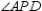 = 63° and m
= 63° and m 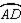 = 75°, find m
= 75°, find m  .
.
(Short Answer)
4.9/5  (34)
(34)
Externally tangent circles P and Q touch at point T and have the line of centers 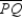 . How does one construct the common internal tangent for circles P and Q?
. How does one construct the common internal tangent for circles P and Q?
(Essay)
4.9/5  (36)
(36)
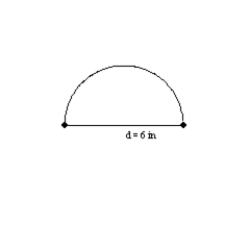 -What is the exact volume for the solid that results when the semicircular region shown is rotated about its diameter of length 6 inches?
-What is the exact volume for the solid that results when the semicircular region shown is rotated about its diameter of length 6 inches?
(Essay)
4.8/5  (34)
(34)
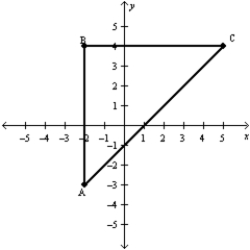 -Find the area of
-Find the area of  , which has vertices at A(-2,-3), B(-2,4) and C(5,4).
, which has vertices at A(-2,-3), B(-2,4) and C(5,4).
(Multiple Choice)
4.9/5  (31)
(31)
 -In
-In 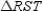 (not shown),
(not shown), 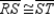 . Which statement is not necessarily true?
. Which statement is not necessarily true?
(Multiple Choice)
4.7/5  (36)
(36)
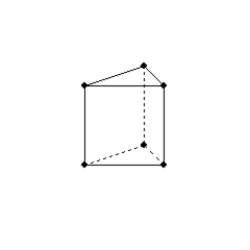 -A prism and pyramid have congruent bases and the same length of altitude. If the volume of the pyramid is 24
-A prism and pyramid have congruent bases and the same length of altitude. If the volume of the pyramid is 24  , find the volume of the prism.
, find the volume of the prism.
(Essay)
4.9/5  (31)
(31)
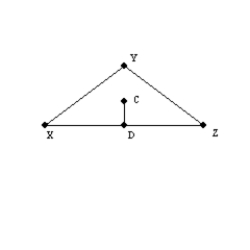 -Which of the following lines (line segments) are concurrent?
-Which of the following lines (line segments) are concurrent?
(Multiple Choice)
4.8/5  (31)
(31)
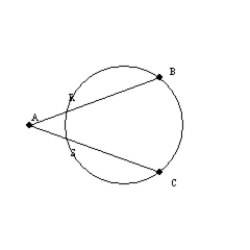 -In the figure, secants
-In the figure, secants 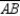 and
and 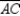 intersect the circle at points R and S respectively. If m
intersect the circle at points R and S respectively. If m  = 36° and m
= 36° and m 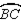 : m
: m 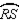 = 4:1, find m
= 4:1, find m 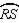 .
.
(Short Answer)
4.7/5  (35)
(35)
In Cartesian space, the point (0,6,0) lies 6 units above the origin.
(True/False)
4.8/5  (31)
(31)
Showing 101 - 120 of 916
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)