Exam 7: Locus and Concurrence
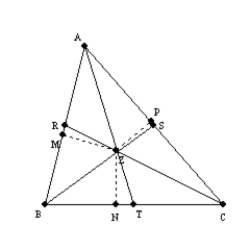 -Use the drawing provided to explain the following theorem.
"The three angle bisectors of the angles of a triangle are concurrent."
Given:
-Use the drawing provided to explain the following theorem.
"The three angle bisectors of the angles of a triangle are concurrent."
Given: 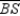 ,
,  , and
, and 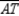 are the angle bisectors of the angles of
are the angle bisectors of the angles of 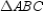 Prove:
Prove: 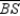 ,
,  , and
, and 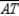 are concurrent at point Z
are concurrent at point Z
Let point Z name the point of intersection of the angle bisectors 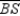 and
and  . Because
. Because 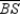 bisects
bisects 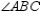 , every point on
, every point on  (including Z) is equidistant from the sides of
(including Z) is equidistant from the sides of  .
.
With 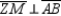 and
and 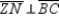 , it follows that
, it follows that 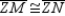 . With respect to
. With respect to 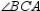 , also note
, also note
that 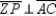 . Because Z lies on angle bisector
. Because Z lies on angle bisector  , we also have
, we also have 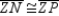 . By the Transitive Property of Congruence,
. By the Transitive Property of Congruence, 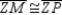 . With point Z being equidistant from the sides of
. With point Z being equidistant from the sides of 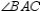 , Z must also lie on angle bisector
, Z must also lie on angle bisector 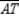 . Thus,
. Thus, 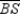 ,
,  , and
, and 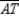 are concurrent at point Z.
are concurrent at point Z.
 -Supply missing reasons for the following proof.
Given:
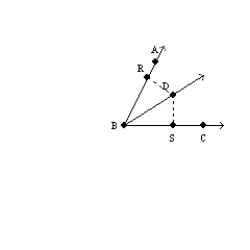
-Supply missing reasons for the following proof.
Given: 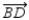 bisects
bisects 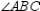 ;
; 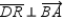 and
and 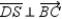 Prove:
Prove: 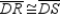 S1.
S1. 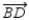 bisects
bisects  ; R1.
; R1. 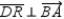 and
and 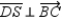 S2.
S2. 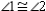 R2.
S3.
R2.
S3. 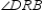 and
and 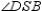 are rt.
are rt.  R3.
S4.
R3.
S4. 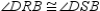 R4.
S5.
R4.
S5. 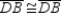 R5.
S6.
R5.
S6. 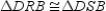 R6.
S7.
R6.
S7. 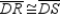 R7.
R7.
R1. Given
R2. Definition of angle-bisector
R3. Perpendicular lines form right angles.
R4. All right angles are congruent.
R5. Identity
R6. AAS
R7. CPCTC
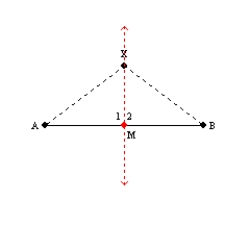 -Supply missing statements and missing reasons for the following proof.
Given: Point X not on
-Supply missing statements and missing reasons for the following proof.
Given: Point X not on 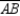 so that
so that 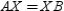 Prove: X lies on the perpendicular-bisector of
Prove: X lies on the perpendicular-bisector of 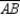 S1. R1.
S2.
S1. R1.
S2. 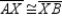 R2.
S3. With M the midpoint of
R2.
S3. With M the midpoint of 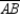 , R3.
draw
, R3.
draw 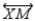 S4. Then
S4. Then 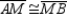 R4.
S5. Also,
R4.
S5. Also, 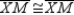 R5.
S6. R6. SSS
S7.
R5.
S6. R6. SSS
S7. 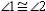 R7.
S8. R8. Definition of perpendicular-bisector of a line segment
R7.
S8. R8. Definition of perpendicular-bisector of a line segment
S1. Point X not on 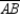 so that
so that 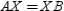 R1. Given
R1. Given
R2. Definition of congruent line segments
R3. Through 2 points, there is exactly one line.
R4. Definition of midpoint of line segment
R5. Identity
S6. 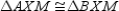 R7. CPCTC
R7. CPCTC
S8. X lies on the perpendicular-bisector of 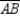
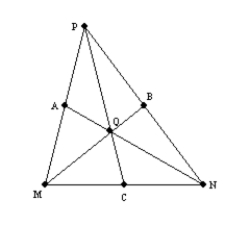 -Use the drawing provided to explain the following.
Given:
-Use the drawing provided to explain the following.
Given: 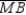 ,
, 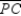 , and
, and 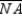 are the medians of
are the medians of 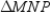 Prove:
Prove: 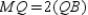
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)