Exam 8: Calculus of Several Variables
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
Sketch the level curves of the function corresponding to the given values of z. 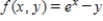 ;
; 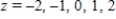
(Multiple Choice)
4.7/5  (37)
(37)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 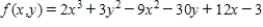
(Multiple Choice)
5.0/5  (26)
(26)
Find the second-order partial derivatives of the function. 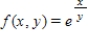
(Multiple Choice)
4.8/5  (35)
(35)
A closed rectangular box having a volume of 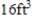 is to be constructed. If the material for the sides costs
is to be constructed. If the material for the sides costs 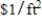 and the material for the top and bottom costs
and the material for the top and bottom costs 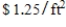 , find the dimensions of the box that can be constructed with minimum cost.
, find the dimensions of the box that can be constructed with minimum cost.
(Multiple Choice)
4.7/5  (36)
(36)
The Country Workshop's total weekly profit (in dollars) realized in manufacturing and selling its rolltop desks is given by the profit function
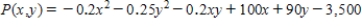
where x stands for the number of finished units and y stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between 180 and 200 and the number of unfinished units varies between 100 and 120 per week. Please round your answer to the nearest dollar, if necessary.
P = $__________ per week.
where x stands for the number of finished units and y stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between 180 and 200 and the number of unfinished units varies between 100 and 120 per week. Please round your answer to the nearest dollar, if necessary.
P = $__________ per week.
(Short Answer)
4.9/5  (29)
(29)
Use a double integral to find the volume of the solid shown in the figure. 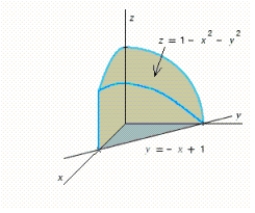
(Multiple Choice)
4.7/5  (35)
(35)
An open rectangular box is to be constructed from material that costs 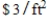 for the bottom and
for the bottom and 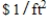 for its sides. Find the dimensions of the box of greatest volume that can be constructed for
for its sides. Find the dimensions of the box of greatest volume that can be constructed for 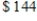 .
.
(Short Answer)
4.9/5  (38)
(38)
Find the volume of the solid bounded above by the surface 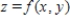
And below by the plane region R.
And below by the plane region R.
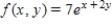
R is the triangle with vertices
R is the triangle with vertices 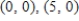 and
and 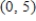 .
.
(Multiple Choice)
4.7/5  (32)
(32)
Find the approximate change in z when the point 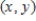 changes from
changes from 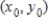 to
to 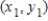 .
. 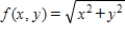 ; from
; from 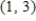 to
to 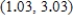
(Multiple Choice)
4.8/5  (28)
(28)
Evaluate the double integral 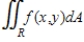
For the given function f(x, y) and the region R.
For the given function f(x, y) and the region R.
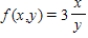 ; R is the rectangle defined by
; R is the rectangle defined by 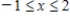 and
and 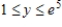
(Multiple Choice)
4.9/5  (40)
(40)
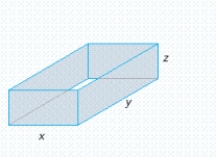
A building in the shape of a rectangular box is to have a volume of 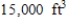 (see the figure). It is estimated that the annual heating and cooling costs will be $2/square foot for the top, $5/square foot for the front and back, and $3/square foot for the sides. Find the dimensions of the building that will result in a minimal annual heating and cooling cost. What is the minimal annual heating and cooling cost(C)?
(see the figure). It is estimated that the annual heating and cooling costs will be $2/square foot for the top, $5/square foot for the front and back, and $3/square foot for the sides. Find the dimensions of the building that will result in a minimal annual heating and cooling cost. What is the minimal annual heating and cooling cost(C)?
(Short Answer)
4.8/5  (31)
(31)
Find the equation of the least-squares line for the given data. Draw a scatter diagram for the given data and graph the least-squares line. 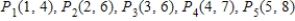
(Multiple Choice)
4.9/5  (35)
(35)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 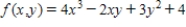
(Multiple Choice)
4.8/5  (31)
(31)
The flow of blood through an arteriole in cubic centimeters per second is given by 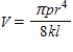
Where l is the length (in cm) of the arteriole, r is its radius (in cm), p is the difference in pressure between the two ends of the arteriole (in dyne/cm2), and k is the viscosity of blood (in dyne-sec/cm2). Find the approximate percentage change in the flow of blood if an error of 4% is made in measuring the length of the arteriole and an error of 3% is made in measuring its radius. Assume that p and k are constant.
Where l is the length (in cm) of the arteriole, r is its radius (in cm), p is the difference in pressure between the two ends of the arteriole (in dyne/cm2), and k is the viscosity of blood (in dyne-sec/cm2). Find the approximate percentage change in the flow of blood if an error of 4% is made in measuring the length of the arteriole and an error of 3% is made in measuring its radius. Assume that p and k are constant.
(Multiple Choice)
4.8/5  (38)
(38)
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false.
The least-squares line must pass through at least one data point.
(Multiple Choice)
4.8/5  (34)
(34)
Use a double integral to find the volume of the solid shown in the figure. 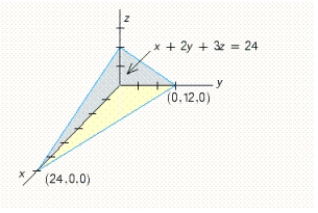
(Multiple Choice)
4.8/5  (24)
(24)
Showing 21 - 40 of 219
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)