Exam 8: Calculus of Several Variables
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
An auxiliary electric power station will serve three communities, A, B, and C, whose relative locations are shown in the accompanying figure. Determine where the power station should be located if the sum of the squares of the distances from each community to the site is minimized. Please round the answer to the nearest hundredth.
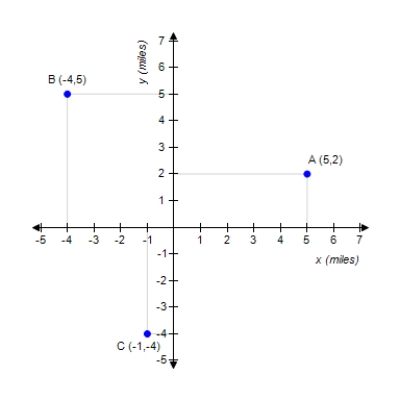
(Short Answer)
4.8/5  (29)
(29)
Find the volume of the solid bounded above by the surface
z = f(x, y)
and below by the plane region R. Enter your answer as an expression.
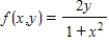 ; R is the region bounded by
; R is the region bounded by 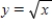 ,
, 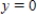 and
and 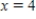 .
.
(Short Answer)
4.8/5  (36)
(36)
Evaluate the double integral 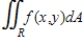
For the given function f(x, y) and the region R.
For the given function f(x, y) and the region R.
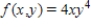 ; R is the rectangle defined by
; R is the rectangle defined by 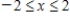 and
and 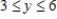 .
.
(Multiple Choice)
4.9/5  (32)
(32)
The Company requires that its corned beef hash containers have a capacity of 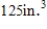 , be right circular cylinders, and be made of a tin alloy. Find the radius and height of the least expensive container that can be made if the metal for the side and bottom costs
, be right circular cylinders, and be made of a tin alloy. Find the radius and height of the least expensive container that can be made if the metal for the side and bottom costs 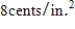 and the metal for the pull-off lid costs
and the metal for the pull-off lid costs 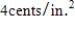 .
.
(Multiple Choice)
4.9/5  (35)
(35)
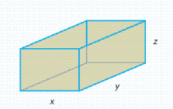
Postal regulations specify that the combined length and girth of a parcel sent by parcel post may not exceed 120 in. Find the dimensions of the rectangular package that would have the greatest possible volume under these regulations. (Hint: Let the dimensions of the box be x'' by y'' by z'' (see the figure below). Then, 2x + 2x + y= 120 , and the volume V=xyz. So that 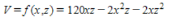 . Maximize f(x,z) .)
. Maximize f(x,z) .)
(Multiple Choice)
5.0/5  (36)
(36)
Find an equation of the least-squares line for the data. Please round the coefficients to the nearest hundredth. x
1
1
2
3
4
4
5
Y
2
3
5
6
6
6)5
8)5
(Multiple Choice)
4.8/5  (32)
(32)
Evaluate the first partial derivatives of the function at the given point. 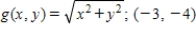
(Multiple Choice)
4.9/5  (37)
(37)
Postal regulations specify that the combined length and girth of a parcel sent by parcel post may not exceed 108 in. Find the dimensions of the rectangular package that would have the greatest possible volume under these regulations.
(Short Answer)
4.7/5  (29)
(29)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 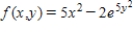
(Multiple Choice)
4.8/5  (34)
(34)
Sketch the level curves of the function corresponding to the given values of z. 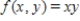 ;
; 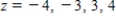
(Multiple Choice)
4.7/5  (29)
(29)
The total weekly revenue (in dollars) of the company realized in manufacturing and selling its rolltop desks is given by
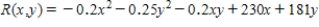
where x denotes the number of finished units and y denotes the number of unfinished units manufactured and sold each week. The total weekly cost attributable to the manufacture of these desks is given by
where x denotes the number of finished units and y denotes the number of unfinished units manufactured and sold each week. The total weekly cost attributable to the manufacture of these desks is given by
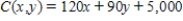
dollars. Determine how many finished units and how many unfinished units the company should manufacture each week in order to maximize its profit. What is the maximum profit(P) realizable?
x = __________
y = __________
P = $__________
dollars. Determine how many finished units and how many unfinished units the company should manufacture each week in order to maximize its profit. What is the maximum profit(P) realizable?
x = __________
y = __________
P = $__________
(Short Answer)
4.9/5  (39)
(39)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 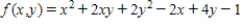
(Multiple Choice)
4.8/5  (40)
(40)
The population density of a certain city is given by the function 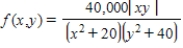
Where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by
Where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by
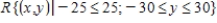
(Multiple Choice)
4.9/5  (38)
(38)
Use a double integral to find the volume of the solid shown in the figure. 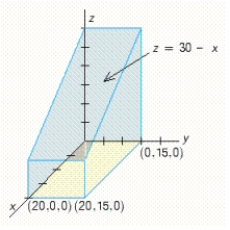
(Multiple Choice)
4.9/5  (40)
(40)
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If the data consist of two distinct points, then the least-squares line is just the line that passes through the two points.
(Essay)
4.9/5  (48)
(48)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function.
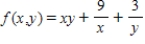
Find the critical point(s) of the function.
Find the point(s) of maximum.
Find the point(s) of minimum.
Find the relative extrema of the function.
Find the critical point(s) of the function.
Find the point(s) of maximum.
Find the point(s) of minimum.
Find the relative extrema of the function.
(Short Answer)
4.9/5  (36)
(36)
Showing 141 - 160 of 219
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)