Exam 8: Calculus of Several Variables
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
The total weekly profit (in dollars) realized by Country Workshop in manufacturing and selling its rolltop desks is given by the profit function
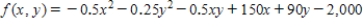
where x stands for the number of finished units and y denotes the number of unfinished units manufactured and sold each week. The company's management decides to restrict the manufacture of these desks to a total of exactly 200 units/week. How many finished and how many unfinished units should be manufactured each week to maximize the company's weekly profit?
where x stands for the number of finished units and y denotes the number of unfinished units manufactured and sold each week. The company's management decides to restrict the manufacture of these desks to a total of exactly 200 units/week. How many finished and how many unfinished units should be manufactured each week to maximize the company's weekly profit?
(Short Answer)
4.8/5  (44)
(44)
Find the approximate change in z when the point 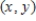 changes from
changes from 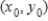 to
to 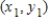 . Round your answer to two decimal places.
. Round your answer to two decimal places.
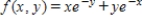 ; from
; from 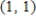 to
to 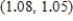
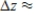 __________
__________
(Short Answer)
4.8/5  (32)
(32)
Find the average value of the function 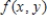 over the plane region R.
over the plane region R. 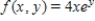 and R is the triangle with vertices
and R is the triangle with vertices 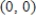 ,
, 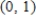 and
and 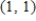 .
.
(Multiple Choice)
4.7/5  (32)
(32)
The total daily profit (in dollars) realized by Weston Publishing in publishing and selling its dictionaries is given by the profit function
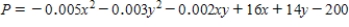
where x stands for the number of deluxe editions and y denotes the number of standard editions sold daily. Weston's management decides that publication of these dictionaries should be restricted to a total of exactly 400 copies/day. How many deluxe copies and how many standard copies should be published each day to maximize Weston's daily profit?
Find the number of deluxe copies.
Find the number of standard copies.
where x stands for the number of deluxe editions and y denotes the number of standard editions sold daily. Weston's management decides that publication of these dictionaries should be restricted to a total of exactly 400 copies/day. How many deluxe copies and how many standard copies should be published each day to maximize Weston's daily profit?
Find the number of deluxe copies.
Find the number of standard copies.
(Short Answer)
4.7/5  (36)
(36)
Find the volume of the solid bounded above by the surface 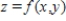
And below by the plane region R.
And below by the plane region R.
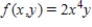 and R is the region bounded by the graphs of
and R is the region bounded by the graphs of  and
and 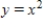 .
.
(Multiple Choice)
4.8/5  (34)
(34)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 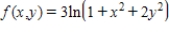
(Multiple Choice)
4.8/5  (36)
(36)
Find the volume of the solid bounded above by the surface
Z = f(x, y)
And below by the plane region R.
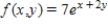 ; R is the triangle with vertices (0, 0), (5, 0) and (0, 5).
; R is the triangle with vertices (0, 0), (5, 0) and (0, 5).
(Multiple Choice)
5.0/5  (41)
(41)
Evaluate the double integral 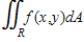
For the given function f(x, y) and the region R.
F(x, y) = 6x + 6y; R is bounded by x = 0,
For the given function f(x, y) and the region R.
F(x, y) = 6x + 6y; R is bounded by x = 0, 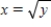 , y = 0 and y = 4.
, y = 0 and y = 4.
(Multiple Choice)
4.9/5  (42)
(42)
Evaluate the double integral 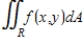 for the given function f(x, y) and the region R. Enter your answer as a fraction. f(x, y) = 2y + 3x; R is the rectangle defined by
for the given function f(x, y) and the region R. Enter your answer as a fraction. f(x, y) = 2y + 3x; R is the rectangle defined by 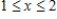 and
and 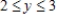 .
.
(Short Answer)
4.8/5  (23)
(23)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 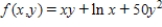
(Multiple Choice)
4.9/5  (30)
(30)
Find the maximum and minimum values of the function 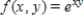
Subject to the constraint
Subject to the constraint 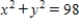 .
.
(Multiple Choice)
4.8/5  (34)
(34)
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function.
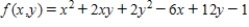
Find the critical point(s) of the function.
Find the point(s) of maximum.
Find the point(s) of minimum.
Find the relative extrema of the function.
Find the critical point(s) of the function.
Find the point(s) of maximum.
Find the point(s) of minimum.
Find the relative extrema of the function.
(Short Answer)
4.8/5  (40)
(40)
Evaluate the double integral 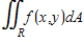 for the given function f(x, y) and the region R. Enter your answer as a fraction. f(x, y) = 4x + 8y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.
for the given function f(x, y) and the region R. Enter your answer as a fraction. f(x, y) = 4x + 8y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.
(Short Answer)
4.9/5  (41)
(41)
Find the approximate change in z when the point 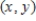 changes from
changes from 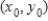 to
to 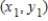 .
.
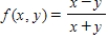 ; from
; from 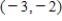 to
to 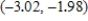
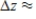 __________
__________
(Short Answer)
4.8/5  (43)
(43)
Evaluate the double integral
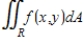
for the given function f(x, y) and the region R. Enter your answer as a fraction.
f(x, y) = 0x + 0y; R is bounded by x = 0,
for the given function f(x, y) and the region R. Enter your answer as a fraction.
f(x, y) = 0x + 0y; R is bounded by x = 0, 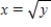 , y = 0 and y = 4.
, y = 0 and y = 4.
(Short Answer)
4.9/5  (34)
(34)
Find the volume of the solid bounded above by the surface 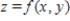 and below by the plane region R.
and below by the plane region R. 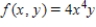 and R is the region bounded by the graphs of
and R is the region bounded by the graphs of 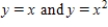 .
.
(Multiple Choice)
4.9/5  (44)
(44)
Showing 121 - 140 of 219
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)