Exam 19: Questions that Involve Online Topics
Exam 1: Introduction145 Questions
Exam 2: Organizing and Visualizing Data210 Questions
Exam 3: Numerical Descriptive Measures153 Questions
Exam 4: Basic Probability171 Questions
Exam 5: Discrete Probability Distributions218 Questions
Exam 6: The Normal Distribution and Other Continuous Distributions191 Questions
Exam 7: Sampling and Sampling Distributions197 Questions
Exam 8: Confidence Interval Estimation196 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests165 Questions
Exam 10: Two-Sample Tests210 Questions
Exam 11: Analysis of Variance213 Questions
Exam 12: Chi-Square Tests and Nonparametric Tests201 Questions
Exam 13: Simple Linear Regression213 Questions
Exam 14: Introduction to Multiple Regression355 Questions
Exam 15: Multiple Regression Model Building96 Questions
Exam 16: Time-Series Forecasting168 Questions
Exam 17: Statistical Applications in Quality Management133 Questions
Exam 18: A Roadmap for Analyzing Data54 Questions
Exam 19: Questions that Involve Online Topics321 Questions
Select questions type
TABLE 19-3
The following information is from 2 investment opportunities. 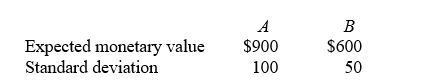 -Referring to Table 19-3, what is the coefficient of variation for investment A?
-Referring to Table 19-3, what is the coefficient of variation for investment A?
(Multiple Choice)
4.7/5  (43)
(43)
The difference between expected payoff under certainty and expected value of the best act without certainty is the
(Multiple Choice)
4.9/5  (47)
(47)
TABLE 19-2
The following payoff matrix is given in dollars. 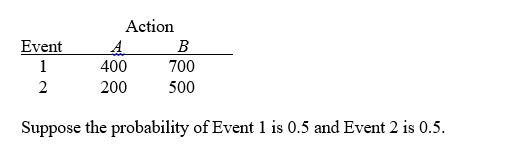 -For a potential investment of $5,000, a portfolio has an EMV of $1,000 and a standard deviation of $100. What is the rate of return?
-For a potential investment of $5,000, a portfolio has an EMV of $1,000 and a standard deviation of $100. What is the rate of return?
(Multiple Choice)
4.9/5  (38)
(38)
TABLE 6-1
A company has 125 personal computers. The probability that any one of them will require repair on a given day is 0.15.
-Referring to Table 6-1, which of the following is one of the properties required so that the binomial distribution can be used to compute the probability that no more than 2 computers will require repair on a given day?
(Multiple Choice)
4.8/5  (41)
(41)
Look at the utility function graphed below and select the type of decision maker that corresponds to the graph. 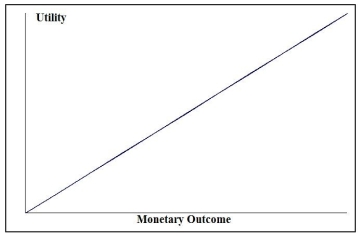
(Multiple Choice)
4.8/5  (37)
(37)
TABLE 6-1
A company has 125 personal computers. The probability that any one of them will require repair on a given day is 0.15.
-Referring to Table 6-1 and assuming that the number of computers that requires repair on a given day follows a binomial distribution, compute the probability that there will be less than 8 computers that require repair on a given day using a normal approximation.
(Short Answer)
5.0/5  (34)
(34)
TABLE 7-1
Times spent studying by students in the week before final exams follow a normal distribution with standard deviation 8 hours. A random sample of 4 students was taken from a population of 50 in order to estimate the mean study time for the population of all students. Use the finite population correction.
-Referring to Table 7-1, 90% of all the samples of 4 will have a sample mean of no more than how many hours from the population mean?
(Short Answer)
4.8/5  (31)
(31)
TABLE 6-1
A company has 125 personal computers. The probability that any one of them will require repair on a given day is 0.15.
-Referring to Table 6-1 and assuming that the number of computers that requires repair on a given day follows a binomial distribution, compute the probability that there will be less than 25 or more than 30 computers that require repair on a given day using a normal approximation.
(Short Answer)
4.7/5  (38)
(38)
TABLE 7-1
Times spent studying by students in the week before final exams follow a normal distribution with standard deviation 8 hours. A random sample of 4 students was taken from a population of 50 in order to estimate the mean study time for the population of all students. Use the finite population correction.
-Referring to Table 7-1, 5% of all the samples of 4 will have a sample mean of at least how many hours above the population mean?
(Short Answer)
4.7/5  (34)
(34)
TABLE 19-5
The following payoff table shows profits associated with a set of 2 alternatives under 3 possible events.  -Referring to Table 19-5, what is the EMV for Action B?
-Referring to Table 19-5, what is the EMV for Action B?
(Short Answer)
4.8/5  (37)
(37)
If a new machine of a production plant is functioning properly, only 1% of the items produced will be defective. Out of the 1,000 items the plant produces on a single day, the approximate probability that exactly 0.2% of the items will be defective if the new machine is indeed functioning properly is ________.
(Short Answer)
4.9/5  (43)
(43)
TABLE 9-1
A manufacturer produces light bulbs that have a mean life of at least 500 hours when the production process is working properly. Based on past experience, the population standard deviation is 50 hours and the light bulb life is normally distributed. The operations manager stops the production process if there is evidence that the population mean light bulb life is below 500 hours.
-Referring to Table 9-1, if you select a sample of 100 light bulbs and are willing to have a level of significance of 0.01, the probability of the operations manager failing to stop the process if the population mean bulb life is 490 hours is ________.
(Short Answer)
4.8/5  (41)
(41)
TABLE 19-2
The following payoff matrix is given in dollars. 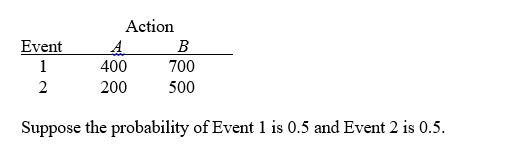 -The minimum expected opportunity loss is also equal to
-The minimum expected opportunity loss is also equal to
(Multiple Choice)
4.7/5  (38)
(38)
As a general rule, one can use the normal distribution to approximate a binomial distribution whenever the sample size is at least 30.
(True/False)
4.8/5  (41)
(41)
TABLE 9-3
A drug company is considering marketing a new local anesthetic. The effective time of the anesthetic the drug company is currently producing has a normal distribution with a mean of 7.4 minutes with a standard deviation of 1.2 minutes. The chemistry of the new anesthetic is such that the effective time should be normally distributed with the same standard deviation. The company will market the new local anesthetic as being better if there is evidence that the population mean effective time is greater than the 7.4 minutes of the current local anesthetic.
-Referring to Table 9-3, if you select a sample of 25 new local anesthetics and are willing to have a level of significance of 0.05, the probability of the company failing to market the new local anesthetic when it is better is ________ if the population mean effective time is 8 minutes.
(Short Answer)
4.8/5  (40)
(40)
TABLE 8-1
A random sample of 100 stores from a large chain of 500 garden supply stores was selected to determine the mean number of lawnmowers sold at an end-of-season clearance sale. The sample results indicated a mean of 6 and a standard deviation of 2 lawnmowers sold. A 95% confidence interval (5.623 to 6.377) was established based on these results.
-Referring to Table 8-1, 95% of the stores have sold between 5.623 and 6.377 lawnmowers.
(True/False)
4.8/5  (35)
(35)
As a general rule, one can use the normal distribution to approximate a binomial distribution whenever nπ and n(π - 1) are at least 5.
(True/False)
4.7/5  (42)
(42)
TABLE 19-1
The following payoff table shows profits associated with a set of 3 alternatives under 2 possible states of nature.  -Referring to Table 19-1, the opportunity loss for A2 when S1 occurs is
-Referring to Table 19-1, the opportunity loss for A2 when S1 occurs is
(Multiple Choice)
4.8/5  (42)
(42)
TABLE 16-1
Given below are the average prices for three types of energy products for five consecutive years. 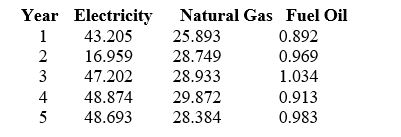 -Referring to Table 16-1, what is the unweighted aggregate price index for the group of three energy items in year 5 using year 1 as the base year?
-Referring to Table 16-1, what is the unweighted aggregate price index for the group of three energy items in year 5 using year 1 as the base year?
(Short Answer)
4.8/5  (44)
(44)
TABLE 19-2
The following payoff matrix is given in dollars. 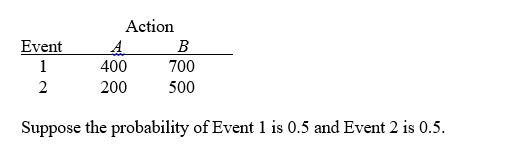 -Referring to Table 19-2, the return to risk ratio for Action B is
-Referring to Table 19-2, the return to risk ratio for Action B is
(Multiple Choice)
4.7/5  (37)
(37)
Showing 141 - 160 of 321
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)