Exam 9: Mathematical Modeling Using Differential Equations
Exam 1: Functions and Change204 Questions
Exam 2: Rate of Change: the Derivative132 Questions
Exam 3: Shortcuts to Differentiation178 Questions
Exam 4: Using the Derivative94 Questions
Exam 5: Accumulated Change: the Definite Integral93 Questions
Exam 6: Antiderivatives and Applications122 Questions
Exam 7: Probability68 Questions
Exam 8: Functions of Several Variables134 Questions
Exam 9: Mathematical Modeling Using Differential Equations121 Questions
Exam 10: Geometric Series65 Questions
Select questions type
The solution to the differential equation 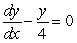 subject to the initial condition
subject to the initial condition 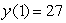 is
is 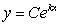 , where k = _____ and C = _____. Round answers to 2 decimal places.
, where k = _____ and C = _____. Round answers to 2 decimal places.
(Short Answer)
4.8/5  (40)
(40)
A cup of green tea contains 32 mg of caffeine when you are using the tea leaves for the first time. A cup from the second brew contains 12 mg of caffeine, while a cup from the third brew contains only 4 mg of caffeine. Caffeine leaves the body at a continuous rate of about 17% per hour.
a) Write a differential equation for the amount, C, of caffeine in the body at time t hours after drinking the green tea.
b) Use the differential equation to find 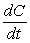 at the start of the first hour (right after drinking the tea) for a cup from the first brew, and use your answer to estimate the change in caffeine in the body during the first hour.
c) Does the initial amount of caffeine in the body (whether from the first, second or third brew) change the differential equation?
at the start of the first hour (right after drinking the tea) for a cup from the first brew, and use your answer to estimate the change in caffeine in the body during the first hour.
c) Does the initial amount of caffeine in the body (whether from the first, second or third brew) change the differential equation?
(Short Answer)
4.7/5  (34)
(34)
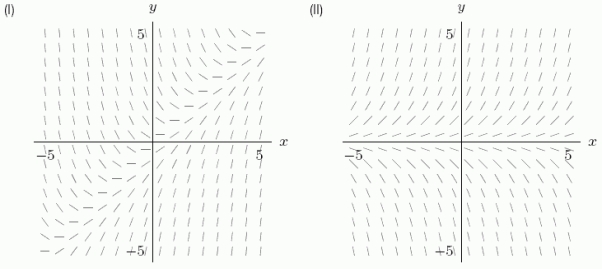
The slope fields for 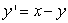 and
and 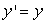 are shown in the following figure. Which slope field goes with the differential equation
are shown in the following figure. Which slope field goes with the differential equation 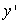 = x
= x 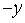 ?
? 
(Short Answer)
4.7/5  (43)
(43)
If the slope field for 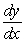 has constant slopes where x is fixed, what do we know about
has constant slopes where x is fixed, what do we know about 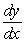 ?
?
(Multiple Choice)
4.8/5  (42)
(42)
If 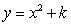 is a solution to the differential equation
is a solution to the differential equation 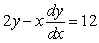 , then k = _____.
, then k = _____.
(Short Answer)
4.9/5  (31)
(31)
Given that 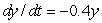 and
and 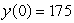 , estimate
, estimate 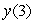 by first estimating y(1) and y(2). Assume that the rate of growth given by
by first estimating y(1) and y(2). Assume that the rate of growth given by 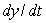 is approximately constant over each unit time interval.
is approximately constant over each unit time interval.
(Short Answer)
4.8/5  (37)
(37)
A quantity y satisfies the differential equation 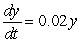 . Thus, y is decreasing when y is ________(less/greater) than _____.
. Thus, y is decreasing when y is ________(less/greater) than _____.
(Short Answer)
4.8/5  (32)
(32)
Sketch a slope field for the differential equation 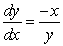 using the points indicated on the axes.
using the points indicated on the axes. 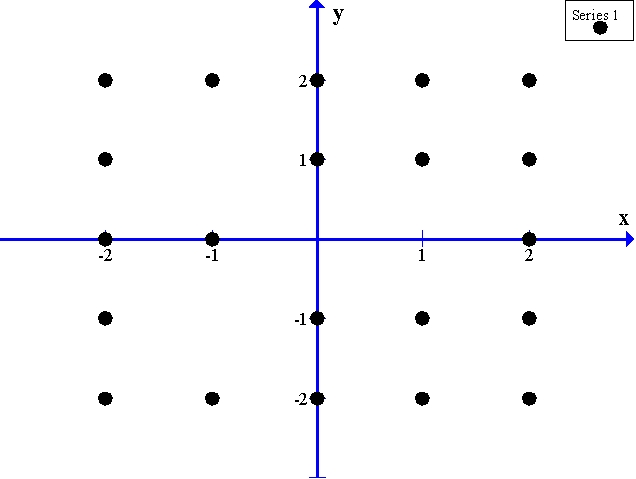
(Essay)
4.7/5  (39)
(39)
Consider the slope field for 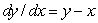 . What is the slope at the point (0,0)?
. What is the slope at the point (0,0)?
(Short Answer)
5.0/5  (43)
(43)
The equilibrium solution for 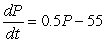 is P = _____. This solution is ________ (stable/unstable).
is P = _____. This solution is ________ (stable/unstable).
(Short Answer)
4.8/5  (34)
(34)
A company earns a continuous annual rate of 11% of its net worth. At the same time, it has expenses of 6.2 million dollars per year. If the company's net worth at time t = 0 is 50 million, how many years will it take to go bankrupt? Round to the nearest year.
(Short Answer)
4.9/5  (36)
(36)
An anti-inflammatory drug has a half-life in the human body of about 8 hours.
A. Use the half-life to find the value of k in the differential equation 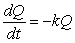 , where Q is the quantity of the drug in the body t hours after the drug is administered. Round to 4 decimal places.
B. After how many hours will 45% of the original dose remain in the body? Round to 2 decimal places.
, where Q is the quantity of the drug in the body t hours after the drug is administered. Round to 4 decimal places.
B. After how many hours will 45% of the original dose remain in the body? Round to 2 decimal places.
(Short Answer)
4.8/5  (35)
(35)
Which one(s) of the following are solutions to the differential equation 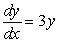 ?
?
(Multiple Choice)
4.8/5  (35)
(35)
What is the solution of the differential equation 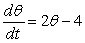 if
if 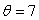 when
when 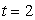 ?
?
(Multiple Choice)
4.9/5  (38)
(38)
What is the threshold value for the strain of the flu modeled by the differential equations 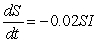
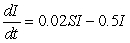 ?
Round to the nearest whole number.
?
Round to the nearest whole number.
(Short Answer)
4.8/5  (36)
(36)
On the slope field for the differential equation 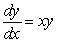 , sketch the solution curve in the fourth quadrant that goes through the point (0, -1).
, sketch the solution curve in the fourth quadrant that goes through the point (0, -1). 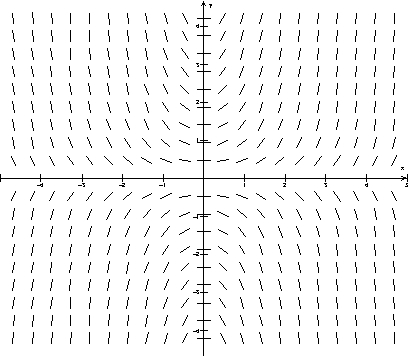
(Short Answer)
4.7/5  (29)
(29)
Consider three strains of the flu modeled by the following sets of differential equations. Which has the infecteds being removed the slowest?
I. 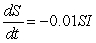
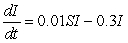 II.
II. 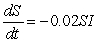
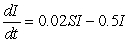 III.
III. 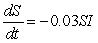
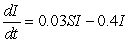
(Short Answer)
4.8/5  (32)
(32)
Owls need trees to survive, but trees don't care one way or the other about owls. Which (if any) of the following systems of differential equations could model the interaction between owls and trees, with trees as x and owls as y? Select all that apply.
(Multiple Choice)
5.0/5  (40)
(40)
Money in a bank account earns interest at a continuous rate of 6% per year, and payments are made continuously out of the account at the rate of $10,000 per year. The account initially contains $100,000. Write a differential equation for the balance, B, in the account in t years and use it to find how many years it will take for the account to run out of money. Round to 1 decimal place.
(Short Answer)
4.8/5  (38)
(38)
Showing 21 - 40 of 121
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)